题目内容
已知函数 ,
, ,且
,且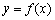 在点
在点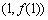 处的切线方程为
处的切线方程为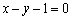 .
.
(Ⅰ)求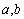 的值;
的值;
(Ⅱ)若函数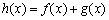 在区间
在区间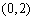 内有且仅有一个极值点,求
内有且仅有一个极值点,求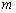 的取值范围;
的取值范围;
(Ⅲ)设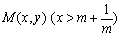 为两曲线
为两曲线 ,
,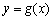 的交点,且两曲线在交点
的交点,且两曲线在交点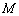 处的切线分别为
处的切线分别为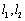 .若取
.若取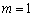 ,试判断当直线
,试判断当直线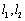 与
与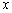 轴围成等腰三角形时
轴围成等腰三角形时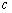 值的个数并说明理由.
值的个数并说明理由.
解:(Ⅰ) ,∴
,∴ ,又
,又 ,
,
∴ . ………………3分
. ………………3分
(Ⅱ) ;
;
∴
由 得
得 ,
,
∴ 或
或 . …………………………………5分
. …………………………………5分
∵ ,当且仅当
,当且仅当 或
或 时,函数
时,函数 在区间
在区间 内有且仅有一个极值点. ………………………6分
内有且仅有一个极值点. ………………………6分
若 ,即
,即 ,当
,当 时
时 ;当
;当 时
时 ,函数
,函数 有极大值点
有极大值点 ,
,
若 ,即
,即 时,当
时,当 时
时 ;当
;当 时
时 ,函数
,函数 有极大值点
有极大值点 ,
,
综上, 的取值范围是
的取值范围是 .……………8分
.……………8分
(Ⅲ)当 时,设两切线
时,设两切线 的倾斜角分别为
的倾斜角分别为 ,
,
则 ,
,
∵ , ∴
, ∴ 均为锐角, ………………………9分
均为锐角, ………………………9分
当 ,即
,即 时,若直线
时,若直线 能与
能与 轴围成等腰三角形,则
轴围成等腰三角形,则 ;当
;当 ,即
,即 时,若直线
时,若直线 能与
能与 轴围成等腰三角形,则
轴围成等腰三角形,则 .
.
由 得,
得, ,
,
得 ,即
,即 ,
,
此方程有唯一解 ,
,
直线 能与
能与 轴围成一个等腰三角形.……11分
轴围成一个等腰三角形.……11分
由 得,
得,  ,
,
得 ,即
,即 ,
,
设 ,
, ,
,
当 时,
时, ,∴
,∴ 在
在 单调递增,
单调递增,
则 在
在 单调递增,由于
单调递增,由于 ,且
,且 ,
,
所以 ,则
,则 ,
,
即方程 在
在 有唯一解,
有唯一解,
直线 能与
能与 轴围成一个等腰三角形.
轴围成一个等腰三角形.
因此,当 时,有两处符合题意,所以直线
时,有两处符合题意,所以直线 能与
能与 轴围成等腰三角形时,
轴围成等腰三角形时, 值的个数有2个. ……………………14分
值的个数有2个. ……………………14分

练习册系列答案
相关题目
 ,则f(2012)=( )
,则f(2012)=( ) D.
D.
 ,
, 满足约束条件
满足约束条件 若目标函数
若目标函数
 的最大值为6,则
的最大值为6,则 的最小值为
的最小值为 B. 3 C. 2 D.4
B. 3 C. 2 D.4 =(1,-2),
=(1,-2), =(a,-1),
=(a,-1), =(-b,0),且A,B,C三点共线,则
=(-b,0),且A,B,C三点共线,则 的最小值为________.
的最小值为________. 
 解集是 ( )
解集是 ( )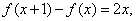 且f(0)=1.
且f(0)=1.
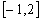 上的最大值。
上的最大值。