题目内容
已知 为常数,函数
为常数,函数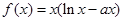 有两个极值点
有两个极值点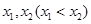 ,则( )
,则( )
A.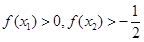 | B.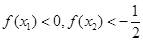 |
C.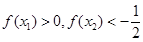 | D.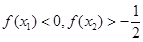 |
D
解析试题分析:求导得: .易得
.易得 在点P(1,0)处的切线为
在点P(1,0)处的切线为 .当
.当 时,直线
时,直线 与曲线
与曲线 交于不同两点(如下图),且
交于不同两点(如下图),且 ,
,
当 时,
时,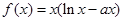 单调递减,当
单调递减,当 时,
时,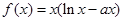 单调递增,
单调递增, 是极小值,
是极小值, 是极大值.
是极大值.  .
. .
.
令 ,则
,则 ,所以
,所以 单调递增,
单调递增, ,即
,即 .
.
考点:导数的应用.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
定义在R上的函数 满足:
满足: 恒成立,若
恒成立,若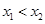 ,则
,则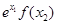 与
与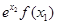 的大小关系为 ( )
的大小关系为 ( )
A. 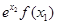 | B.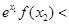 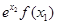 |
C.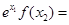 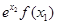 | D.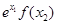 与 与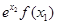 的大小关系不确定 的大小关系不确定 |
已知曲线 的一条切线的斜率为
的一条切线的斜率为 ,则切点的横坐标为( )
,则切点的横坐标为( )
| A.3 | B.2 | C.1 | D. |
定义域为R的连续函数 ,对任意x都有
,对任意x都有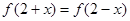 ,且其导函数
,且其导函数 满足
满足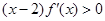 ,则当
,则当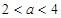 时,有( )
时,有( )
A. | B.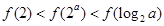 |
C.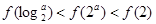 | D.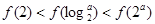 |
设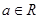 ,函数
,函数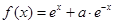 的导函数是
的导函数是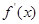 ,且
,且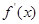 是奇函数。若曲线
是奇函数。若曲线 的一条切线的斜率是
的一条切线的斜率是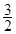 ,则切点的横坐标为( )
,则切点的横坐标为( )
A.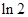 | B.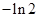 | C.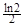 | D.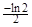 |
已知函数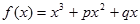 与
与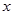 轴相切于
轴相切于 点,且极小值为
点,且极小值为 ,则
,则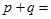 ( )
( )
| A.12 | B.15 | C.13 | D.16 |
已知函数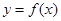 的图像为
的图像为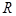 上的一条连续不断的曲线,当
上的一条连续不断的曲线,当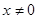 时,
时,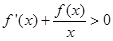 ,则关于
,则关于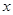 的函数
的函数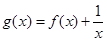 的零点的个数为( )
的零点的个数为( )
| A.0 | B.1 | C.2 | D.0或2 |
定义在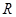 上的函数
上的函数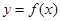 ,满足
,满足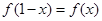 ,
,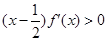 ,若
,若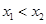 且
且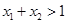 ,则有( )
,则有( )
A.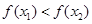 | B.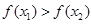 | C.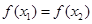 | D.不能确定 |
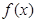 的图象上;②点A、B关于原点对称,则点(A,B)是函数
的图象上;②点A、B关于原点对称,则点(A,B)是函数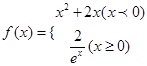 ,则
,则