题目内容

下列结论正确的是（　　）
A、|
a
•
b
|=|
a
|•|
b
|
B、若
a
，
b
都是单位向量，则
a
•
b
≤1恒成立
C、向量
AB
的起点为A（-2，4），总点为B（2，1），则
BA
与x正方向所夹角余弦为
4
5
D、若
a
=（3，m），且|
a
|=4，则m=
7
考点：数量积表示两个向量的夹角,向量的模
专题：平面向量及应用
分析：由向量的夹角和模长的关系，逐个选项验证可得答案．
解答： 解：选项A，|
a
•
b
|=|
a
|•|
b
||cos＜
a
，
b
＞|，只有当|cos＜
a
，
b
＞|=1时，选项A才成立，故A错误；
选项B，∵
a
，
b
都是单位向量，∴
a
•
b
=|
a
|•|
b
|cos＜
a
，
b
＞≤1×1×1=1，故B正确；
选项C，向量
BA
=（-2，4）-（2，1）=（-4，3），∴
BA
与x正方向所夹角余弦为-
4
5
，故C错误；
选项D，若
a
=（3，m），且|
a
|=4，则32+m2=42，解得m=±
7
，故D错误．
故选：B
点评：本题考查向量的夹角和模长，属基础题．
练习册系列答案
相关题目
写出用循环语句描述求
1
6+
1
6+
1
6+
1
6+
1
6+
1
6+
1
6
值的算法程序．
一个几何体的三视图如图所示，则这个几何体的体积为（　　）
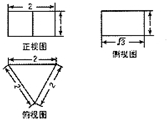
A、
3
B、
3
3
4
C、
3
2
D、2
3
已知数列{an}中，a1=1，且an+an+1=2n，
（1）求数列{an}的通项公式；
（2）若数列{an}的前n项和Sn，求S2n．
一个几何体的三视图如图所示，如该几何体的表面积为92cm2，则h的值为（　　）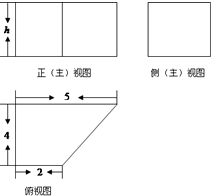
A、4B、5C、6D、7
如图，直三棱柱ABC-A1B1C1中，D，E分别是AB，BB1的中点，AA1=AC=CB=
2
2
AB．
（1）证明：BC1∥平面A1CD；
（2）求二面角A1-EC-C1的余弦值．
已知函数y=x2-2x在P点的切线平行于x轴，求P点的坐标．
已知函数f（x）=
3
sin
x
2
cos
x
2
+cos2
x
2
-
1
2
，△ABC三个内角A，B，C的对边分别为a，b，c．
（1）若x∈[-
π
2
，
π
2
]，求f（x）的值域；
（2）若f（B+C）=1，a=
3
，b=1，求△ABC的面积．
正项数列{an}中，a1=1，an+1-
an+1
=an+
an

（1）数列{
an
}是否为等差数列？说明理由
（2）求an．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网