题目内容
16.倾斜角为$\frac{π}{3}$的直线l过抛物线y2=ax(a>0)的焦点F,且与抛物线交于点A、B,l交抛物线的准线于点C(B在A、C之间),若$|{BC}|=\frac{8}{3}$,则a=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 求得焦点即准线方程.根据三角形的相似关系,求得2丨EF丨=丨CF丨,根据抛物线的定义,即可求得a的值.
解答 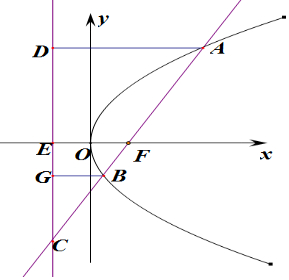 解:过A和D做AD⊥l,BG⊥l,垂足分别为D和G,准线l交x轴于E,
解:过A和D做AD⊥l,BG⊥l,垂足分别为D和G,准线l交x轴于E,
由抛物线的焦点($\frac{a}{4}$,0),准线方程x=-$\frac{a}{4}$,
则丨EF丨=$\frac{a}{2}$,且丨BG丨=丨BF丨,
由∠AFx=$\frac{π}{3}$,则∠FCD=$\frac{π}{6}$,
sin∠FCD=$\frac{丨BG丨}{丨BC丨}$=$\frac{丨EF丨}{丨CF丨}$=$\frac{1}{2}$,
$|{BC}|=\frac{8}{3}$,则丨BG丨=$\frac{4}{3}$,
由2丨EF丨=丨CF丨,即2×$\frac{a}{2}$=丨BC丨+丨BF丨=$\frac{8}{3}$+$\frac{4}{3}$=4,
故a=4,
故选:D.
点评 本题考查抛物线的定义,直线与抛物线的位置关系,相似三角形的性质,考查计算能力,数形结合思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知复数$z=\frac{1}{1+i}$,则z的虚部为( )
| A. | $\frac{1}{2}i$ | B. | $-\frac{1}{2}i$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
5.已知函数f(x)=log2x,x∈[1,8],则不等式1≤f(x)≤2成立的概率是( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
6.设F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点,双曲线上存在一点P使得∠F1PF2=60°,|OP|=3b(O为坐标原点),则该双曲线的离心率为( )
| A. | $\frac{4}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{7}{6}$ | D. | $\frac{\sqrt{42}}{6}$ |
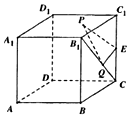 如右图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点,点P,Q分别为面A1B1C1D1和线段B1C上的动点,则△PEQ周长的最小值为$\sqrt{10}$.
如右图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点,点P,Q分别为面A1B1C1D1和线段B1C上的动点,则△PEQ周长的最小值为$\sqrt{10}$.