题目内容
如图,四棱锥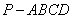 的底面
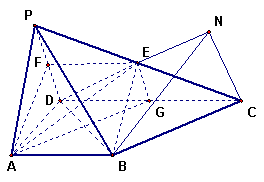
的底面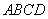 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中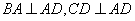 ,
, ,平面
,平面 底面
底面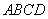 ,
, 是
是 的中点.
的中点.
(1)求证: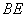 //平面
//平面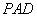 ;
;
(2)求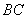 与平面BDE所成角的余弦值;
与平面BDE所成角的余弦值;
(3)线段PC上是否存在一点M,使得AM⊥平面PBD,如果存在,求出PM的长度;如果不存在,请说明理由。

解 (1)取PD中点F,连接AF, EF
则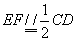 ,
,
又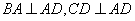 ,
,
 ∴
∴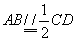
∴
∴四边形ABEF是平行四边形
∴AF∥BE 又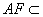 平面PAD,
平面PAD, 平面PAD
平面PAD
∴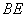 //平面
//平面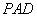
(2)过C作DE的垂线,交DE的延长线于N,连接BN
∵平面 底面
底面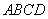 ,
,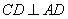
∴ 平面
平面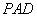
∴ AF 又AF⊥PD,
AF 又AF⊥PD,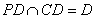
∴AF⊥平面PCD
∴BE⊥平面PCD
∴BE⊥CN,又CN⊥DE,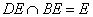
∴CN⊥平面BDE
∴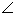 CBN就是直线
CBN就是直线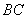 与平面BDE所成角
与平面BDE所成角
令AD=1,,易求得 ,
,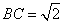
∴sin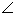 CBN=
CBN=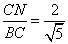
∴cos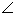 CBN=
CBN=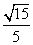
故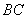 与平面BDE所成角的余弦值为
与平面BDE所成角的余弦值为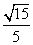
(3)假设PC上存在点M,使得AM⊥平面PBD 则AM⊥PD,由(2)AF⊥PD
∴PD⊥平面AFM,又PD⊥平面ABEF
故点M与E重合。
取CD中点G,连接EG,AG
易证BD⊥AG,又BD⊥AE
∴BD⊥平面AEG
∴BD⊥EG
∴BD⊥PD,又PD⊥CD
∴PD⊥平面BCD
从而PD⊥AD,这与⊿PAD是等边三角形矛盾
故PC上不存在点M满足题意。

练习册系列答案
相关题目
 ,则满足
,则满足 的
的 的取值范围是
的取值范围是
 满足
满足 ,则
,则 的最小值为 。
的最小值为 。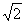 B.
B.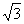 C.
C.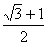 D.
D.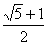
 ·
· 的值为( )
的值为( ) C.
C. D.
D.
 (a>0,且a≠1)的图象可能是( )
(a>0,且a≠1)的图象可能是( )