题目内容
1.函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-4,x≤0}\\{-{x}^{2}+2x+lnx,x>0}\end{array}\right.$的零点个数是3.分析 分段讨论,当x≤0时,解得x=-2,即f(x)在(-∞,0]上有1个零点,当x>0时,在同一坐标系中,作出y=lnx与y=x2-2x,根据图象,易知有2个交点,即可求出零点的个数.
解答 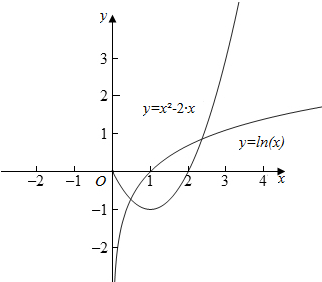 解:当x≤0时,f(x)=x2-4=0,解得x=-2,即f(x)在(-∞,0]上有1个零点,
解:当x≤0时,f(x)=x2-4=0,解得x=-2,即f(x)在(-∞,0]上有1个零点,
当x>0时,f(x)=-x2+2x+lnx=0,即lnx=x2-2x,
分别画出y=lnx与y=x2-2x(x>0)的图象,如图所示:
由图象可知道函数y=lnx,与函y=x2-2x有2个交点,
函数f(x)=-x2+2x+lnx(x>0)的零点有2个,
综上所述,f(x)的零点有3个,
故答案为:3.
点评 本题主要考查了函数的零点的个数的判断,解题中注意体会数形结合思想与转化思想在解题中的应用.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
9.《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额.此项税款按下表分段累计计算:
(1)设某人月工资、薪金所得为x元,求应纳税款Y的函数表达式?
(2)某人一月份应交纳此项税款为303元,那么他当月的工资,薪金所得是多少?
| 全月应纳税所得额 | 税率(%) |
| 不超过1500元的部分 | 3 |
| 超过1500元至4500元的部分 | 10 |
| 超过4500元至9000元的部分 | 20 |
(2)某人一月份应交纳此项税款为303元,那么他当月的工资,薪金所得是多少?
16.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=3x+m(m为常数),则f(log3$\frac{1}{5}$)=( )
| A. | 4 | B. | -4 | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
 如图所示,由直线x=a,x=a+1(a>0),y=x2及x轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即a2<${∫}_{a}^{a+1}$x2dx<(a+1)2.类比之,?n∈N*,$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$<A<$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,则实数A=ln2.
如图所示,由直线x=a,x=a+1(a>0),y=x2及x轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即a2<${∫}_{a}^{a+1}$x2dx<(a+1)2.类比之,?n∈N*,$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$<A<$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,则实数A=ln2.