题目内容
△ABC中,∠A=60°,点D在边AC上,DB=
,且
=λ(
+
)(λ>0),则AC+AB的最大值为 .
| 3 |
| BD |
| ||
|
|
| ||
|
|
考点:平面向量的基本定理及其意义
专题:解三角形,平面向量及应用
分析:根据
=λ(
+
)容易判断点D为AC的中点,所以在△ABD中,由余弦定理得:3=AB2+AD2-2AB•ADcos∠A,将AD=
AC,∠A=60°带入并整理以及根据基本不等式可得,4AB2+AC2-12=2AB•AC≤AB2+AC2,(AB=AC时取“=“),这样即可求得AB,AC的最大值,所以求得AC+AB的最大值.
| BD |
| ||
|
|
| ||
|
|
| 1 |
| 2 |
解答:
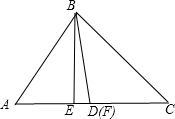
解:如图,过B作BE⊥AC,垂足为E,取AC中点F,连接BF,则:
=λ(
+
)=
(
+
)=
;
∴
与
共线,∴D点和F点重合,∴D是AC的中点;
∴在△ABD中由余弦定理得:3=AB2+AD2-2AB•ADcos60°=AB2+(
AC)2-AB•(
AC)=AB2+
AC2-
AB•AC;
∴4AB2+AC2-12=2AB•AC≤AB2+AC2,∴AB2≤4,(当且仅当AB=AC时取“=“);
∴AB最大为2,此时AC取最大2,∴AC+AB的最大值为4.

| BD |
| ||
| |BE| |
| ||
| |BE| |
| λ |
| |BE| |
| BA |
| BC |
| 2λ |
| |BE| |
| BF |
∴
| BD |
| BF |
∴在△ABD中由余弦定理得:3=AB2+AD2-2AB•ADcos60°=AB2+(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
∴4AB2+AC2-12=2AB•AC≤AB2+AC2,∴AB2≤4,(当且仅当AB=AC时取“=“);
∴AB最大为2,此时AC取最大2,∴AC+AB的最大值为4.
点评:考查向量加法的平行四边形法则,共线向量基本定理,余弦定理,基本不等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目