题目内容
14.已知$α∈(\frac{π}{2},π)$,且tanα=-3.(1)求$sin(\frac{π}{4}+α)$的值;
(2)求$cos(\frac{2π}{3}-2α)$的值.
分析 (1)由已知利用同角三角函数基本关系式即可计算得解.
(2)利用二倍角公式可求sin2α,cos2α的值,进而利用两角差的余弦函数公式即可计算得解.
解答 解:(1)因为$α∈(\frac{π}{2},π)$,tanα=-3,
可得$sinα=\frac{{3\sqrt{10}}}{10}$,$cosα=-\frac{{\sqrt{10}}}{10}$,
可得:$sin(\frac{π}{4}+α)=\frac{{\sqrt{2}}}{2}(sinα+cosα)=\frac{{\sqrt{2}}}{2}×(\frac{{3\sqrt{10}}}{10}-\frac{{\sqrt{10}}}{10})=\frac{{\sqrt{5}}}{5}$.
(2)sin2α=2sinαcosα=-$\frac{3}{5}$,cos2α=cos2α-sin2α=-$\frac{4}{5}$,
可得:$cos(\frac{2π}{3}-2α)$=cos$\frac{2π}{3}$cos2α+sin$\frac{2π}{3}$sin2α=$\frac{4-3\sqrt{3}}{10}$.
点评 本题主要考查了同角三角函数基本关系式,二倍角公式,两角差的余弦函数公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
相关题目
10.若f(x)=-x2+2(a-1)x+2在(-∞,4]上单调递增,则实数a的取值范围是( )
| A. | a≥-3 | B. | a≤-3 | C. | a≤5 | D. | a≥5 |
19.下列关于直观图的叙述正确的是( )
| A. | 正三角形的直观图是正三角形 | B. | 平行四边形的直观图是平行四边形 | ||
| C. | 矩形的直观图是矩形 | D. | 圆的直观图是圆 |
6.设角α的终边经过点(-6t,-8t) (t≠0),则sin α-cos α的值是( )
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | ±$\frac{1}{5}$ | D. | 不确定 |
3.已知关于x的一元二次不等式ax2+bx+c>0的解集为{x|-2<x<3},则不等式cx2-bx+a<0的解集是( )
| A. | {x|x$<-\frac{1}{2}$或x$>\frac{1}{3}$} | B. | {x|x$\frac{1}{3}$或x>$\frac{1}{2}$} | C. | {x|-$\frac{1}{2}$<x<$\frac{1}{3}$} | D. | {x|-$\frac{1}{3}$<x<$\frac{1}{2}$} |
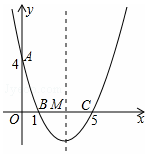 如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x 轴相交于点M.
如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x 轴相交于点M.