题目内容
已知函数f（x）=3x2-1在区间（0，1）上有唯一零点x0，如果用“二分法”求这个零点（精确度ε=0.05）的近似值，那么将区间（0，1）等分的次数至少是 ，此时并规定只要零点的存在区间（a，b）满足|a-b|＜ε时，用
作为零点的近似值，那么求得x0= ．
| a+b |
| 2 |
考点：二分法求方程的近似解
专题：函数的性质及应用
分析：根据计算精确度与区间长度和计算次数的关系满足
＜精确度确定．
| b-a |
| 2n |
解答：
解：开区间（0，1）的长度等于1，每经过一次操作，区间长度变为原来的一半，经过n此操作后，
区间长度变为
，故有
≤0.05，
即2n＞20，因为25=32，所以n=5．
故计算5次就可满足要求，
所以将区间（0，1）等分的次数至多是5次．
因为f（
）＜0，所以第一次得到区间为（
，1）；
因为f（
）＞0，所以第二次得到区间为（
，
）；
因为f（
）＞0，所以第三次得到区间为（
，
）；
因为f（
）＜0，所以第四次得到区间为（
，
）；
因为f（
）＞0，所以第五次得到区间为（
，
）；
所以函数零点为
=
；
故答案为：5；
区间长度变为
| 1 |
| 2n |
| 1 |
| 2n |
即2n＞20，因为25=32，所以n=5．
故计算5次就可满足要求，
所以将区间（0，1）等分的次数至多是5次．
因为f（
| 1 |
| 2 |
| 1 |
| 2 |
因为f（
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
因为f（
| 5 |
| 8 |
| 1 |
| 2 |
| 5 |
| 8 |
因为f（
| 9 |
| 16 |
| 9 |
| 16 |
| 5 |
| 8 |
因为f（
| 19 |
| 32 |
| 9 |
| 16 |
| 19 |
| 32 |
所以函数零点为
| ||||
| 2 |
| 37 |
| 64 |
故答案为：5；
| 37 |
| 64 |
点评：本题考查了二分法求方程的根；在用二分法求方程的近似解时，精确度与区间长度和计算次数之间存在紧密的联系，可以根据其中两个量求得另一个．设须计算n次，则n满足
＜精确度即可．
| b-a |
| 2n |
练习册系列答案
相关题目
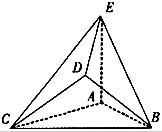在如图所示的几何体中，是边长为2的正三角形，AE＞1，AE⊥平面ABC，平面BCD⊥平面ABC，BD=CD，且BD⊥CD．
如图，在四面体ABCD中，CB=CD，AD⊥BD，点E，F分别是AB，BD的中点