题目内容
下列说法正确的是
①用最小二乘法求的线性回归直线
=bx+a必过点(
,
)
②一批产品共50件,其中5件次品,其余均为合格品,现从中任取2件,则其中出现次品的概率为
③两人独立地解决同一个问题,甲解决这个问题的概率为P1,乙解决这个问题的概率为P2,两人同时解决的概率为P3,则这个问题得到解决的概率等于P1+P2-P3,也等于1-(1-P1)(1-P2)
④已知随机变量ξ服从正态分布N(2,σ2),P(ξ≤4)=0.84,则P(ξ≤0)=0.16
⑤对于空间任意一点O和不共线的三点A、B、C,若
=x
+y
+z
(x,y,z∈R),则P、A、B、C四点共面的充要条件是x+y+z=1.
①用最小二乘法求的线性回归直线
| ∧ |
| y |
. |
| x |
. |
| y |
②一批产品共50件,其中5件次品,其余均为合格品,现从中任取2件,则其中出现次品的概率为
| ||||
|
③两人独立地解决同一个问题,甲解决这个问题的概率为P1,乙解决这个问题的概率为P2,两人同时解决的概率为P3,则这个问题得到解决的概率等于P1+P2-P3,也等于1-(1-P1)(1-P2)
④已知随机变量ξ服从正态分布N(2,σ2),P(ξ≤4)=0.84,则P(ξ≤0)=0.16
⑤对于空间任意一点O和不共线的三点A、B、C,若
| OP |
| OA |
| OB |
| OC |
考点:命题的真假判断与应用,最小二乘法,正态分布曲线的特点及曲线所表示的意义
专题:常规题型,概率与统计
分析:①回归直线过样本点的中心,②用古典概型概率公式概率;③独立事件的同时发生的概率为它们的概率之积,对立事件概率之和为1;④利用正态分布及概率性质得答案;⑤要分充分性与必要性证明.
解答:
解:回归直线过样本点的中心,故①正确;
一批产品共50件,其中5件次品,其余均为合格品,现从中任取2件,则其中出现次品的概率为
+
;故②不正确;
独立事件的同时发生的概率为它们的概率之积,两人都解决不了的概率为(1-P1)•(1-P2),则这个问题得到解决的概率也等于1-(1-P1)(1-P2),故③正确;
P(ξ>=4)=1-0.84=0.16,图象对称轴为x=2,则P(ξ<=0)=P(ξ>=4)=0.16,故④正确,
“充分性”
由x+y+z=1,则z=1-x-y,则
=x
+y
+z
=x
+y
+(1-x-y)
=x(
-
)+y(
-
)+
;
即
-
=x(
-
)+y(
-
);
即
=x
+y
;
则P、A、B、C四点共面;
“必要性”
∵则P、A、B、C四点共面,
∴存在x,y,使
=x
+y
;
即
-
=x(
-
)+y(
-
);
即
=x(
-
)+y(
-
)+
=x
+y
+(1-x-y)
=x
+y
+z
;
则1-x-y=z,
即x+y+z=1.
故⑤正确.
故答案为①③④⑤.
一批产品共50件,其中5件次品,其余均为合格品,现从中任取2件,则其中出现次品的概率为
| ||||
|
| ||
|
独立事件的同时发生的概率为它们的概率之积,两人都解决不了的概率为(1-P1)•(1-P2),则这个问题得到解决的概率也等于1-(1-P1)(1-P2),故③正确;
P(ξ>=4)=1-0.84=0.16,图象对称轴为x=2,则P(ξ<=0)=P(ξ>=4)=0.16,故④正确,
“充分性”
由x+y+z=1,则z=1-x-y,则
| OP |
| OA |
| OB |
| OC |
=x
| OA |
| OB |
| OC |
=x(
| OA |
| OC |
| OB |
| OC |
| OC |
即
| OP |
| OC |
| OA |
| OC |
| OB |
| OC |
即
| CP |
| CA |
| CB |
则P、A、B、C四点共面;
“必要性”
∵则P、A、B、C四点共面,
∴存在x,y,使
| CP |
| CA |
| CB |
即
| OP |
| OC |
| OA |
| OC |
| OB |
| OC |
即
| OP |
| OA |
| OC |
| OB |
| OC |
| OC |
=x
| OA |
| OB |
| OC |
=x
| OA |
| OB |
| OC |
则1-x-y=z,
即x+y+z=1.
故⑤正确.
故答案为①③④⑤.
点评:本题考查了回归直线,概率,正态分布及向量等,考查内容很全面,属于中档题.

练习册系列答案
相关题目
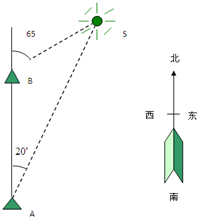 如图,一艘船以32.2n mile/h的速度向正北航行.在A处看灯塔S在船的北偏东20°的方向,30min后航行到B处,在B处看灯塔在船的北偏东65°的方向,已知距离此灯塔6.5n mile以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?
如图,一艘船以32.2n mile/h的速度向正北航行.在A处看灯塔S在船的北偏东20°的方向,30min后航行到B处,在B处看灯塔在船的北偏东65°的方向,已知距离此灯塔6.5n mile以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?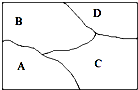 如图,要给地图A、B、C、D四个区域分别涂上红、黄、蓝3种颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有
如图,要给地图A、B、C、D四个区域分别涂上红、黄、蓝3种颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有