题目内容
5.已知△ABC的三边a,b,c所对的角分别为A,B,C且sinA:sinB:sinC=2:3:4.若△ABC的面积为12$\sqrt{15}$,则△ABC的外接圆的半径R=$\frac{32\sqrt{15}}{15}$.分析 根据题意,可以设a=2t,b=3t,c=4t,由余弦定理可得cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=-$\frac{1}{4}$,进而可得sinC=$\frac{\sqrt{15}}{4}$,由正弦定理可得关系式$\frac{1}{2}$absinC=12$\sqrt{15}$,代入数据解可得t=4,可得c的值,由正弦定理2R=$\frac{c}{sinC}$可得R的值.
解答 解:根据题意,由正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R,而sinA:sinB:sinC=2:3:4,
可以设a=2t,b=3t,c=4t,
则cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=-$\frac{1}{4}$,则sinC=$\frac{\sqrt{15}}{4}$,
又由△ABC的面积为12$\sqrt{15}$,
则有$\frac{1}{2}$absinC=12$\sqrt{15}$,即$\frac{1}{2}$×2t×3t×$\frac{\sqrt{15}}{4}$=12$\sqrt{15}$,
解可得t=4,
则c=4t=16;
又由2R=$\frac{c}{sinC}$=$\frac{16}{\frac{\sqrt{15}}{4}}$,解可得R=$\frac{32\sqrt{15}}{15}$;
故答案为:$\frac{32\sqrt{15}}{15}$.
点评 本题考查正弦定理、余弦定理的运用,解题的关键是依据题意结合正弦定理找到三边与外接圆的半径R的关系.

练习册系列答案
相关题目
14.直线y=kx-1(k∈R)与圆(x-1)2+y2=4所截得的弦为AB,则|AB|的最小值是( )
| A. | 2$\sqrt{2}$ | B. | 2 | C. | 3 | D. | 4 |
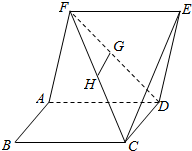 如图.已知正方形ABCD与ADEF边长都为1,且平面ADEF⊥平面ABCD,G,H是DF,FC的中点.
如图.已知正方形ABCD与ADEF边长都为1,且平面ADEF⊥平面ABCD,G,H是DF,FC的中点.