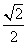题目内容
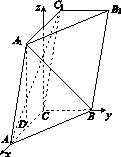
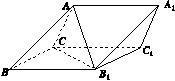
如图11所示,三棱柱ABC A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
(1)证明:AC1⊥A1B;
(2)设直线AA1与平面BCC1B1的距离为 ,求二面角A1 AB C的大小.
,求二面角A1 AB C的大小.
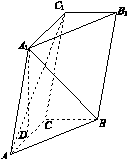
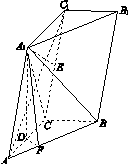
解:方法一:(1)证明:因为A1D⊥平面ABC,A1D⊂平面AA1C1C,故平面AA1C1C⊥平面ABC.
又BC⊥AC,所以BC⊥平面AA1C1C.
连接A1C,因为侧面AA1C1C为菱形,故AC1⊥A1C.
由三垂线定理得AC1⊥A1B.
(2)BC⊥平面AA1C1C,BC⊂平面BCC1B1,故平面AA1C1C⊥平面BCC1B1.
作A1E⊥CC1,E为垂足,则A1E⊥平面BCC1B1.
又直线AA1∥平面BCC1B1,因而A1E为直线AA1与平面BCC1B1的距离,
即A1E= .
.
因为A1C为∠ACC1的平分线,
所以A1D=A1E= .
.
作DF⊥AB,F为垂足,连接A1F.
由三垂线定理得A1F⊥AB,故∠A1FD为二面角A1 AB C的平面角.
由AD= =1,得D为AC中点,
=1,得D为AC中点,
DF=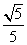 ,tan∠A1FD=
,tan∠A1FD=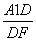 =
=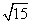 ,所以cos∠A1FD=
,所以cos∠A1FD=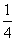 .
.
所以二面角A1 AB C的大小为arccos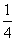 .
.
方法二:以C为坐标原点,射线CA为x轴的正半轴,以CB的长为单位长,建立如图所示的空间直角坐标系C xyz.由题设知A1D与z轴平行,z轴在平面AA1C1C内.
(1)证明:设A1(a,0,c).由题设有a≤2,A(2,0,0),B(0,1,0),则 =(-2,1,0),
=(-2,1,0), =(-2,0,0),
=(-2,0,0), =(a-2,0,c),
=(a-2,0,c), =
=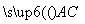 +
+ =(a-4,0,c),
=(a-4,0,c), =(a,-1,c).由|
=(a,-1,c).由| |=2,得
|=2,得 =2,即a2-4a+c2=0.①
=2,即a2-4a+c2=0.①
又 ·
· =a2-4a+c2=0,所以AC1⊥A1B .
=a2-4a+c2=0,所以AC1⊥A1B .
(2)设平面BCC1B1的法向量m=(x,y,z),则m⊥ ,m⊥
,m⊥ ,即m·
,即m· =0,m·
=0,m· =0.因为
=0.因为 =(0,1,0),
=(0,1,0), =
= =(a-2,0,c),所以y=0且(a-2)x+cz=0.
=(a-2,0,c),所以y=0且(a-2)x+cz=0.
令x=c,则z=2-a,所以m=(c,0,2-a),故点A到平面BCC1B1的距离为| |·|cos〈m,
|·|cos〈m, 〉|=
〉|= =
= =c.
=c.
又依题设,A到平面BCC1B1的距离为 ,
,
所以c= ,
,
代入①,解得a=3(舍去)或a=1,
于是 =(-1,0,
=(-1,0, ).
).
设平面ABA1的法向量n=(p,q,r),
则n⊥ ,n⊥
,n⊥ ,即n·
,即n· =0,n·
=0,n· =0,
=0,
-p+ r=0,且-2p+q=0.
r=0,且-2p+q=0.
令p= ,则q=2
,则q=2  ,r=1,所以n=(
,r=1,所以n=( ,2
,2  ,1).
,1).
又p=(0,0,1)为平面ABC的法向量,故
cos〈n,p〉=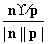 =
=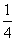 .
.
所以二面角A1 AB C的大小为arccos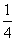 .
.

为了参加2014年青奥会高中篮球比赛,某中学决定从四个篮球较强的班级中选出12人组成男子篮球队代表所在地区参赛,队员来源人数如下表:
| 班级 | 高三(7)班 | 高三(17)班 | 高二(31)班 | 高二(32)班 |
| 人数 | 4 | 2 | 3 | 3 |
(1)从这12名队员中随机选出两名,求两人来自同一班级的概率;
(2)该中学篮球队经过奋力拼搏获得冠军.若要求选出两位队员代表冠军队发言,设其中来自高三(7)班的人数为ξ,求随机变量ξ的分布列.
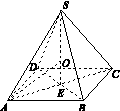
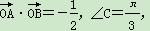 ,从圆O内随机取一个点M,若点M取自△ABC内的概率恰为
,从圆O内随机取一个点M,若点M取自△ABC内的概率恰为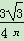 ,则△ABC的形状为( )
,则△ABC的形状为( )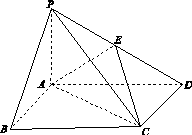
 B.16π C.9π D.
B.16π C.9π D.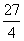
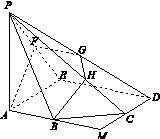
 的正方形ABCD沿对角线BD折起,连接AC,得到三棱锥C ABD,其正视图、俯视图为全等的等腰直角三角形(如图X243所示),则其侧视图的面积为( )
的正方形ABCD沿对角线BD折起,连接AC,得到三棱锥C ABD,其正视图、俯视图为全等的等腰直角三角形(如图X243所示),则其侧视图的面积为( )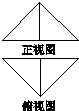
 B.
B. C.1 D.
C.1 D.