题目内容
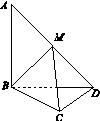
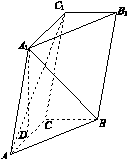
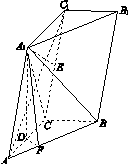
如图15,三棱柱ABC A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.
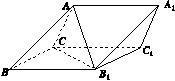
图15
(1)证明:AC=AB1;
(2)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角A A1B1 C1的余弦值.
解:(1)证明:连接BC1,交B1C于点O,连接AO,因为侧面BB1C1C为菱形,所以B1C⊥BC1,且O为B1C及BC1的中点.
又AB⊥B1C,所以B1C⊥平面ABO.
由于AO⊂平面ABO,故B1C⊥AO.
又B1O=CO,故AC=AB1.
(2)因为AC⊥AB1,且O为B1C的中点,所以AO=CO.
又因为AB=BC,所以△BOA≌ △BOC.故OA⊥OB,从而OA,OB,OB1两两垂直.
以O为坐标原点,OB的方向为x轴正方向,|OB|为单位长,建立如图所示的空间直角坐标系O xyz.
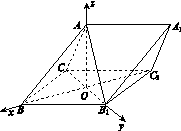
因为∠CBB1=60°,所以△CBB1为等边三角形,又AB=BC,则A ,B(1,0,0),B1
,B(1,0,0),B1 ,C
,C .
.
 =
= ,
,
 =AB=
=AB= ,
,
 1=BC=
1=BC= .
.
设n=(x,y,z)是平面AA1B1的法向量,则
 即
即
所以可取n=(1, ,
, ).
).
设m是平面A1B1C1的法向量,
则
同理可取m=(1,- ,
, ).
).
则cos〈n,m〉= =
= .
.
所以结合图形知二面角A A1B1 C1的余弦值为 .
.

 名校课堂系列答案
名校课堂系列答案低碳生活,从“衣食住行”开始.在国内一些网站中出现了“碳足迹”的应用,人们可以由此计算出自己每天的碳排放量,如家居用电的二氧化碳排放量(kg)=耗电度数×0.785,家用天然气的二氧化碳排放量(kg)=天然气使用立方数×0.19等.某校开展“节能减排,保护环境,从我做起!”的活动,该校高一(六)班同学利用假期在东城、西城两个小区进行了逐户的关于“生活习惯是否符合低碳排放标准”的调查.生活习惯符合低碳观念的称为“低碳家庭”,否则称为“非低碳家庭”.经统计,这两类家庭占各自小区总户数的比例P数据如下:
| 东城小区 | 低碳家庭 | 非低碳家庭 |
| 比例P |
|
|
| 西城小区 | 低碳家庭 | 非低碳家庭 |
| 比例P |
|
|
(1)如果在东城、西城两个小区内各随机选择2个家庭,求这4个家庭中恰好有两个家庭是“低碳家庭”的概率;
(2)该班同学在东城小区经过大力宣传节能减排的重要意义,每周“非低碳家庭”中有20%的家庭能加入到“低碳家庭”的行列中.宣传两周后随机地从东城小区中任选5个家庭,记ξ表示5个家庭中“低碳家庭”的个数,求E(ξ)和D(ξ).
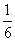 B.
B.
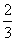 D.
D.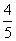



 .
.
 B.
B.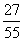
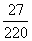 D.
D.