题目内容
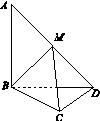
如图13,正方形AMDE的边长为2,B,C分别为AM,MD的中点.在五棱锥P ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.
(1)求证:AB∥FG;
(2)若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长.
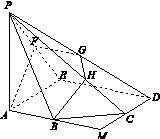
图13
解:(1)证明:在正方形AMDE中,因为B是AM的中点,所以AB∥DE.
又因为AB⊄平面PDE,
所以AB∥平面PDE.
因为AB⊂平面ABF,且平面ABF∩平面PDE=FG,
所以AB∥FG.
(2)因为PA⊥底面ABCDE,
所以PA⊥AB,PA⊥AE.
建立空间直角坐标系Axyz,如图所示,则A(0,0,0),B(1,0,0),C(2,1,0),P(0,0,2),F(0,1,1),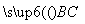 =(1,1,0).
=(1,1,0).
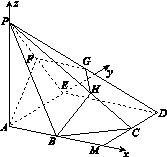
设平面ABF的法向量为n=(x,y,z),则
 .
.
即(u,v,w-2)=λ(2,1,-2),所以u=2λ,v=λ,w=2-2λ.
因为n是平面ABF的一个法向量,


练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 B.
B.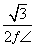
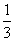 D.
D.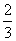
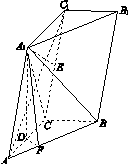
 ,求二面角A1 AB C的大小.
,求二面角A1 AB C的大小.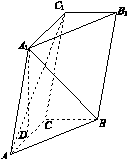
 B.
B.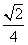
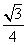 D.
D.
 .
.
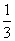 B.
B. C.
C.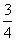 D.
D.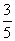
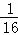 a)的定义域为R,命题q:q:不等式
a)的定义域为R,命题q:q:不等式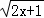 <1+ax对一切正实数x均成立.如果,命题“p∨q”为真命题,命题“p∧q”为假命题,则实数a的取值范围为( )
<1+ax对一切正实数x均成立.如果,命题“p∨q”为真命题,命题“p∧q”为假命题,则实数a的取值范围为( )