题目内容
10.定义在R上的偶函数f(x),对任意x0∈[0,+∞)总存在正实数d,有$\frac{f({x}_{0}+d)-f({x}_{0})}{d}$<0,则( )| A. | f(3)<f(-2)<f(1) | B. | f(1)<f(-2)<f(3) | C. | f(-2)<f(1)<f(3) | D. | f(3)<f(1)<f(-2) |
分析 根据条件判断函数的单调性,利用函数奇偶性和单调性的关系进行转化判断即可.
解答 解:∵任意x0∈[0,+∞)总存在正实数d,有$\frac{f({x}_{0}+d)-f({x}_{0})}{d}$<0,
∴当x≥0时,函数为减函数,
∵函数f(x)是偶函数,∴f(3)<f(2)<f(1),
即f(3)<f(-2)<f(1),
故选:A.
点评 本题主要考查函数值的大小比较,根据条件判断函数的单调性,以及利用函数奇偶性和单调性的关系是解决本题的关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
18.“c=6”是“函数f(x)=x(x-c)2在x=2处有极大值”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.已知随机变量ξ~B(n,p),且E(ξ)=12,D(ξ)=2.4,则n与p的值分别是( )
| A. | 15,$\frac{4}{5}$ | B. | 18,$\frac{2}{3}$ | C. | 20,$\frac{3}{5}$ | D. | 24,$\frac{1}{2}$ |
2.若集合A={x|-1≤x≤3},B={x|x>2},则A∩B=( )
| A. | {x|2<x≤3} | B. | {x|x≥-1} | C. | {x|2≤x<3} | D. | {x|x>2} |
11.下列说法正确的是( )
| A. | 命题“?x∈R,使得x2+x+1≥0”的否定是“?x∈R,使得x2+x+1≥0” | |
| B. | 实数x>y是x2>y2成立的充要条件 | |
| C. | 设p,q为简单命题,若“p∨q”为假命题,则“¬p∧¬q”也为假命题 | |
| D. | 命题“若cosα≠1,则α≠0”为真命题 |
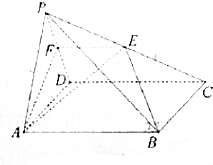 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°,点E是棱PC的中点,平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°,点E是棱PC的中点,平面ABE与棱PD交于点F. 棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,求图中三角形(正四面体的截面)的面积.
棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,求图中三角形(正四面体的截面)的面积.