题目内容
20.已知$sin({\frac{π}{2}-α})=-\frac{4}{5}$,α为第二象限角,则$tan\frac{α}{2}$=3.分析 利用诱导公式求得cosα的值,利用同角三角函数的基本关系求得sinα的值,再利用半角的三角函数的计算公式求得tan$\frac{α}{2}$的值.
解答 解:∵已知$sin({\frac{π}{2}-α})=-\frac{4}{5}$=cosα,α为第二象限角,∴sinα=$\sqrt{{1-cos}^{2}α}$=$\frac{3}{5}$,
则$tan\frac{α}{2}$=$\frac{1-cosα}{sinα}$=3,
故答案为:3.
点评 本题主要考查诱导公式,同角三角函数的基本关系,半角的三角函数的计算公式,三角函数在各个象限中的符号,属于基础题.

练习册系列答案
相关题目
15.方程cosx=lg|x|的实数根的个数是( )
| A. | 2个 | B. | 4个 | C. | 6个 | D. | 7个 |
5.“φ=0”是“函数y=cos(x+φ)为偶函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.下面有段演绎推理:
“直线平行于平面,则该直线平行于平面内所有直线;
已知直线b?平面α,直线a?平面α,直线b∥平面α,
则直线b∥直线a”,则该推理中( )
“直线平行于平面,则该直线平行于平面内所有直线;
已知直线b?平面α,直线a?平面α,直线b∥平面α,
则直线b∥直线a”,则该推理中( )
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 该推理是正确的 |
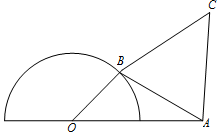 半圆O直径为2,OA=2,B为半圆上任意一点,C为半圆外异于A的点,以AB为边按顺时针方向作正△ABC,问B在何位置时,四边形OACB面积最大?
半圆O直径为2,OA=2,B为半圆上任意一点,C为半圆外异于A的点,以AB为边按顺时针方向作正△ABC,问B在何位置时,四边形OACB面积最大?