题目内容
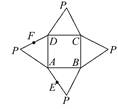
(2013•重庆)如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=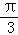 ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.
(1)求PA的长;
(2)求二面角B﹣AF﹣D的正弦值.
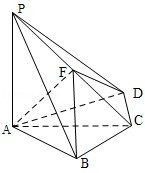
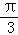 ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.(1)求PA的长;
(2)求二面角B﹣AF﹣D的正弦值.

(1)2 (2)
(2)
 (2)
(2)
(1)如图,连接BD交AC于点O
∵BC=CD,AC平分角BCD,∴AC⊥BD
以O为坐标原点,OB、OC所在直线分别为x轴、y轴,
建立空间直角坐标系O﹣xyz,
则OC=CDcos =1,而AC=4,可得AO=AC﹣OC=3.
=1,而AC=4,可得AO=AC﹣OC=3.
又∵OD=CDsin =
= ,
,
∴可得A(0,﹣3,0),B( ,0,0),C(0,1,0),D(﹣
,0,0),C(0,1,0),D(﹣ ,0,0)
,0,0)
由于PA⊥底面ABCD,可设P(0,﹣3,z)
∵F为PC边的中点,∴F(0,﹣1, ),由此可得
),由此可得 =(0,2,
=(0,2, ),
),
∵ =(
=( ,3,﹣z),且AF⊥PB,
,3,﹣z),且AF⊥PB,
∴ •
• =6﹣
=6﹣ =0,解之得z=2
=0,解之得z=2 (舍负)
(舍负)
因此, =(0,0,﹣2
=(0,0,﹣2 ),可得PA的长为2
),可得PA的长为2 ;
;
(2)由(1)知 =(﹣
=(﹣ ,3,0),
,3,0), =(
=( ,3,0),
,3,0), =(0,2,
=(0,2, ),
),
设平面FAD的法向量为 =(x1,y1,z1),平面FAB的法向量为
=(x1,y1,z1),平面FAB的法向量为 =(x2,y2,z2),
=(x2,y2,z2),
∵ •
• =0且
=0且 •
• =0,∴
=0,∴ ,取y1=
,取y1= 得
得 =(3,
=(3, ,﹣2),
,﹣2),
同理,由 •
• =0且
=0且 •
• =0,解出
=0,解出 =(3,﹣
=(3,﹣ ,2),
,2),
∴向量 、
、 的夹角余弦值为cos<
的夹角余弦值为cos< ,
, >=
>= =
= =
=
因此,二面角B﹣AF﹣D的正弦值等于 =
=

∵BC=CD,AC平分角BCD,∴AC⊥BD
以O为坐标原点,OB、OC所在直线分别为x轴、y轴,
建立空间直角坐标系O﹣xyz,
则OC=CDcos
 =1,而AC=4,可得AO=AC﹣OC=3.
=1,而AC=4,可得AO=AC﹣OC=3.又∵OD=CDsin
 =
= ,
,∴可得A(0,﹣3,0),B(
 ,0,0),C(0,1,0),D(﹣
,0,0),C(0,1,0),D(﹣ ,0,0)
,0,0)由于PA⊥底面ABCD,可设P(0,﹣3,z)
∵F为PC边的中点,∴F(0,﹣1,
 ),由此可得
),由此可得 =(0,2,
=(0,2, ),
),∵
 =(
=( ,3,﹣z),且AF⊥PB,
,3,﹣z),且AF⊥PB,∴
 •
• =6﹣
=6﹣ =0,解之得z=2
=0,解之得z=2 (舍负)
(舍负)因此,
 =(0,0,﹣2
=(0,0,﹣2 ),可得PA的长为2
),可得PA的长为2 ;
;(2)由(1)知
 =(﹣
=(﹣ ,3,0),
,3,0), =(
=( ,3,0),
,3,0), =(0,2,
=(0,2, ),
),设平面FAD的法向量为
 =(x1,y1,z1),平面FAB的法向量为
=(x1,y1,z1),平面FAB的法向量为 =(x2,y2,z2),
=(x2,y2,z2),∵
 •
• =0且
=0且 •
• =0,∴
=0,∴ ,取y1=
,取y1= 得
得 =(3,
=(3, ,﹣2),
,﹣2),同理,由
 •
• =0且
=0且 •
• =0,解出
=0,解出 =(3,﹣
=(3,﹣ ,2),
,2),∴向量
 、
、 的夹角余弦值为cos<
的夹角余弦值为cos< ,
, >=
>= =
= =
=
因此,二面角B﹣AF﹣D的正弦值等于
 =
=


练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
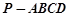 的底面
的底面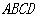 是平行四边形,
是平行四边形,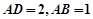 ,
,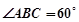 ,
,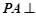 面
面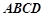 ,设
,设 为
为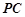 中点,点
中点,点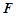 在线段
在线段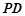 上且
上且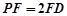 .
.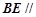 平面
平面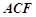 ;
;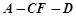 的大小为
的大小为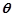 ,若
,若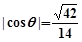 ,求
,求 的长.
的长.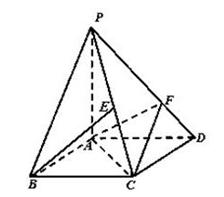
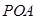 ,
,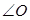 为直角,
为直角,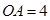 ,
,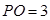 ,现以其中一直角边
,现以其中一直角边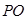 为轴,按逆时针方向旋转
为轴,按逆时针方向旋转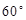 后,将
后,将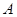 点所在的位置记为
点所在的位置记为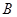 ,再按逆时针方向继续旋转
,再按逆时针方向继续旋转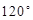 后,
后,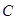 .
.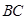 ,取
,取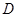 ,求证:面
,求证:面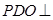 面
面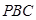 ;
;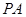 与平面
与平面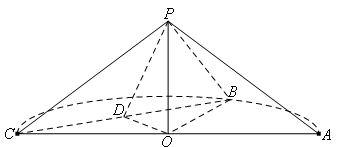
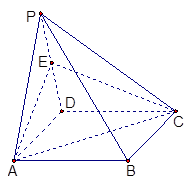
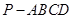 中,底面
中,底面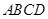 是正方形,侧面
是正方形,侧面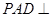 底面
底面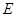 ,
, 分别为
分别为 ,
, 中点,求证:
中点,求证: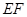 ∥平面
∥平面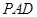 ;
;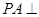
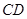 ;
;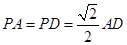 ,求证:平面
,求证:平面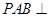 平面
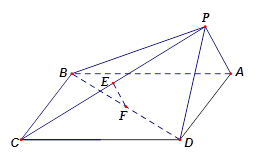
平面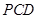 .
.
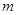 ,
,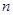 是不重合的两条直线,
是不重合的两条直线,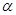 ,
,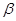 是不重合的两个平面.下列命题:①若
是不重合的两个平面.下列命题:①若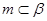 ,则
,则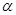 ,
,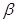 是两个不同的平面.则下列命题中正确的是( )
是两个不同的平面.则下列命题中正确的是( )
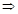
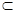 α,则m//α
α,则m//α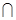 β="m," n⊥m ,则n⊥α.
β="m," n⊥m ,则n⊥α.