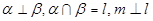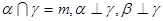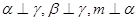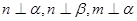题目内容
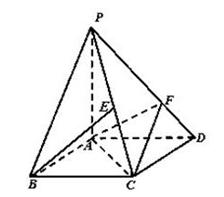
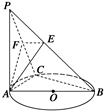
如图,四棱锥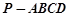 的底面
的底面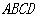 是平行四边形,
是平行四边形,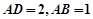 ,
,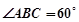 ,
,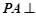 面
面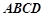 ,设
,设 为
为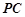 中点,点
中点,点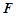 在线段
在线段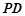 上且
上且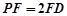 .
.
(1)求证: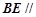 平面
平面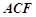 ;
;
(2)设二面角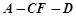 的大小为
的大小为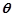 ,若
,若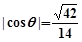 ,求
,求 的长.
的长.
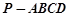 的底面
的底面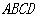 是平行四边形,
是平行四边形,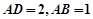 ,
,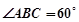 ,
,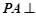 面
面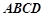 ,设
,设 为
为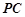 中点,点
中点,点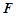 在线段
在线段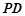 上且
上且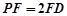 .
.(1)求证:
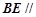 平面
平面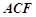 ;
;(2)设二面角
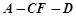 的大小为
的大小为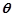 ,若
,若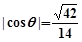 ,求
,求 的长.
的长.
(1)证明详见解析;(2)2 .
试题分析:(1)由已知条件用余弦定理和勾股定理推导出AB⊥AC.又PA⊥面ABCD,以AB,AC,AP分别为x,y,z轴建立坐标系.利用向量法能求出BE∥平面ACF.
(2)分别求出面PCD法向量和面ACF的法向量,由
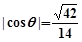 ,利用向量法能求出PA的长.
,利用向量法能求出PA的长.(1)由
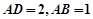 ,
,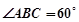 得
得 ,
,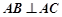 .
.又
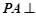 面
面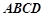 ,所以以
,所以以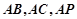 分别为
分别为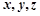 轴建立坐标系如图.
轴建立坐标系如图.则
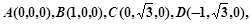 2分
2分设
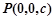 ,则
,则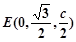 .
.设
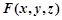 ,
,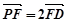 得:
得: .
.解得:
 ,
, ,
,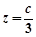 ,
,所以
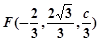 . 4分
. 4分所以
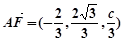 ,
,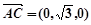 ,
,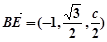 .
.设面
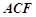 的法向量为
的法向量为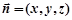 ,则
,则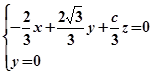 ,取
,取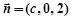 .
.因为
 ,且
,且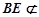 面
面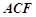 ,所以
,所以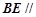 平面
平面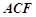 . 6分
. 6分(2)设面
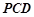 法向量为
法向量为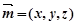 ,因为
,因为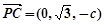 ,
,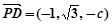 ,
,所以
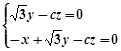 ,取
,取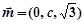 . 9分
. 9分由
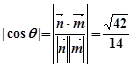 ,得
,得 .
. ,得
,得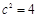 ,∴
,∴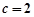 ,所以
,所以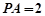 . 12分
. 12分
练习册系列答案
相关题目
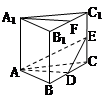
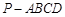 ,底面
,底面 为矩形,侧棱
为矩形,侧棱 ,其中
,其中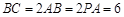 ,
,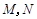 为侧棱
为侧棱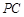 上的两个三等分点,如下图所示.
上的两个三等分点,如下图所示.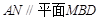 ;
;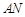 与
与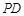 所成角的余弦值;
所成角的余弦值;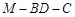 的余弦值.
的余弦值.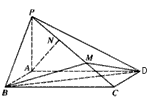
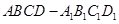 中,底面ABCD和侧面
中,底面ABCD和侧面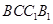 都是矩形,E是CD的中点,
都是矩形,E是CD的中点,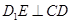 ,
,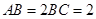 .
.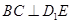 ;
;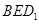 所成的锐二面角的大小为
所成的锐二面角的大小为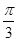 ,求线段
,求线段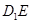 的长度.
的长度.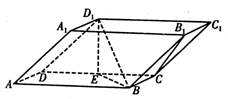

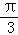 ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.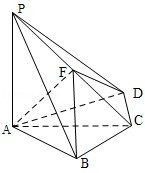
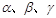 为平面,
为平面,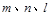 为直线,以下四组条件,可以作为
为直线,以下四组条件,可以作为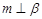 的一个充分条件的是( )
的一个充分条件的是( )