题目内容
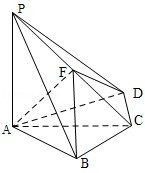
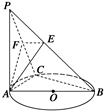
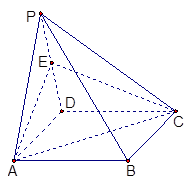
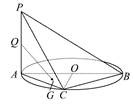
如图,四棱锥P -ABCD的底面是矩形,侧面PAD是正三角形,且侧面PAD⊥底面ABCD,E 为侧棱PD的中点。
(1)证明:PB//平面EAC;
(2)若AD="2AB=2," 求直线PB与平面ABCD所成角的正切值;
(1)证明:PB//平面EAC;
(2)若AD="2AB=2," 求直线PB与平面ABCD所成角的正切值;

(1)详见解析;(2)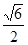 .
.
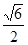 .
.试题分析:(1)要证
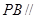 平面
平面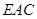 ,根据线面平行的判定定理,只需证明
,根据线面平行的判定定理,只需证明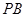 平行于平面
平行于平面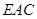 中的一条直线.连接
中的一条直线.连接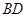 交
交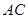 于
于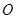 ,连接
,连接 ,因为
,因为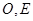 分别为
分别为 的中点,根据三角形的中位线的性质,可知
的中点,根据三角形的中位线的性质,可知 ,从而问题得证;
,从而问题得证;(2)设
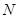 为
为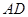 中点,连接
中点,连接 ,则
,则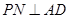 ,从而可得
,从而可得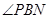 为直线
为直线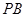 与平面
与平面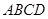 所成的角,进而可求
所成的角,进而可求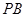 与平面
与平面 所成角正切值;
所成角正切值;解:(1)连结BD交AC于O,连结EO,
因为O、E分别为BD、PD的中点, 所以EO//PB, 2分
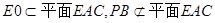 ,所以PB//平面EAC。 5分
,所以PB//平面EAC。 5分(2)设N为AD中点,连接PN,则
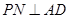 6分
6分又面PAD⊥底面ABCD,所以,PN⊥底面ABCD 7分
所以
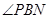 为直线PB与平面ABCD所成的角, 8分
为直线PB与平面ABCD所成的角, 8分
 又AD=2AB=2,则PN=
又AD=2AB=2,则PN=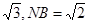 , 10分
, 10分所以tan
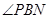 =
= , 12分;所以PB与平面ABCD所成角正切为值
, 12分;所以PB与平面ABCD所成角正切为值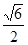 13分
13分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
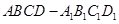 中,底面ABCD和侧面
中,底面ABCD和侧面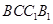 都是矩形,E是CD的中点,
都是矩形,E是CD的中点,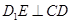 ,
,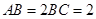 .
.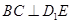 ;
;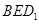 所成的锐二面角的大小为
所成的锐二面角的大小为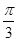 ,求线段
,求线段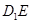 的长度.
的长度.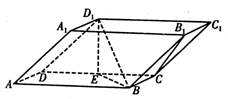
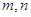 为异面直线,
为异面直线, 平面
平面 ,
, 平面
平面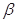 .平面α与β外的直线
.平面α与β外的直线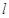 满足
满足 ,则( )
,则( ) ,且
,且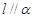
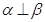 ,且
,且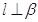

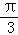 ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.