题目内容
定义函数f(x)=m*x,其中m*x=
(1)若m=
,函数y=f(x)-a在区间[1,2]内存在零点,则实数a的取值范围是 ;
(2)设M=e*a+e*b,N=2e*
,则M,N的大小关系是 .
|
(1)若m=
| 1 |
| 2 |
(2)设M=e*a+e*b,N=2e*
| a+b |
| 2 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:(1)直接根据所给的函数进行处理,结合指数函数的图象进行求解,(2)则结合基本不等式求解.
解答:
解:(1)因为m=
,
令函数y=f(x)-a=0,
得到f(x)=a,
∵x∈[1,2],
∴f(x)∈[
,1],
∴a∈[
,1].
(2)∵M=e*a+e*b,N=2e*
,
当a,b<0时,
M=N,
当a,b>0时,
M>N,
故M≥N.
故答案为:(1)[
,1];(2)M≥N.
| 1 |
| 2 |
令函数y=f(x)-a=0,
得到f(x)=a,
∵x∈[1,2],
∴f(x)∈[
| 1 |
| 4 |
∴a∈[
| 1 |
| 4 |
(2)∵M=e*a+e*b,N=2e*
| a+b |
| 2 |
当a,b<0时,
M=N,
当a,b>0时,
M>N,
故M≥N.
故答案为:(1)[
| 1 |
| 4 |
点评:本题重点考查了指数函数的图象与性质、基本不等式等知识属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
和函数g(x)=acos(
x+
)-a+1(a>0),若存在x1,x2∈[0,1]使得f(x1)=g(x2),则实数a的取值范围是( )
|
| π |
| 6 |
| π |
| 3 |
| A、(0,1] |
| B、[1,2] |
| C、(0,2] |
| D、[2,+∞) |
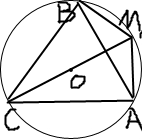 如图,在△ABC中,a,b,c分别为∠A,∠B,∠C的对边,a2+b2-c2=ab,CM是△ABC外接圆的直径,BM=11,AM=2,求CM的长.
如图,在△ABC中,a,b,c分别为∠A,∠B,∠C的对边,a2+b2-c2=ab,CM是△ABC外接圆的直径,BM=11,AM=2,求CM的长. 某篮球队甲、乙两名队员,在预赛中每场比赛得分的原始记录如右茎叶图所示,若要从甲、乙两人中选拔一人参加决赛,则应该选择
某篮球队甲、乙两名队员,在预赛中每场比赛得分的原始记录如右茎叶图所示,若要从甲、乙两人中选拔一人参加决赛,则应该选择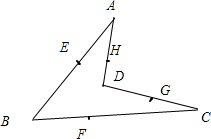 如图,A,B,C,D为不共面的四点,E,F,G,H分别在线段AB,BC,CD,DA上.
如图,A,B,C,D为不共面的四点,E,F,G,H分别在线段AB,BC,CD,DA上.