题目内容
9.已知数列{an}中,${a_1}=2,{a_{n+1}}=2{a_n}-2n+2,n∈{N^*}$.(Ⅰ)记bn=an-2n,求数列{bn}的通项公式;
(Ⅱ)设数列{an}的前n项的和为Sn,数列{cn}满足${c_n}=\frac{1}{{{S_{n+1}}}}+\frac{1}{{{S_{n+2}}}}+…+\frac{1}{{{S_{2n}}}}$,若对任意的正整数n,当m∈[-2,4]时,不等式6t2-12mt+1>6cn恒成立,求实数t的取值范围.
分析 (I)由${a_1}=2,{a_{n+1}}=2{a_n}-2n+2,n∈{N^*}$,变形为an+1-2(n+1)=2[an-2n],bn=an-2n,即bn+1=2bn,即可得出.
(II)由(I)可得:bn=an-2n=0,解得an=2n,可得数列{an}的前n项的和为Sn=n2+n.可得$\frac{1}{{S}_{n}}$=$\frac{1}{n}-\frac{1}{n+1}$.利用“裂项求和”可得cn.可得(cn)max.根据对任意的正整数n,当m∈[-2,4]时,不等式6t2-12mt+1>6cn恒成立,即可得出.
解答 解:(I)∵${a_1}=2,{a_{n+1}}=2{a_n}-2n+2,n∈{N^*}$,
∴an+1-2(n+1)=2[an-2n],bn=an-2n,
∴bn+1=2bn,
而b1=a1-2=0,
可得bn=0.
(II)由(I)可得:bn=an-2n=0,解得an=2n,
∴数列{an}的前n项的和为Sn=$\frac{n(2+2n)}{2}$=n2+n.
∴$\frac{1}{{S}_{n}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$.
∴${c_n}=\frac{1}{{{S_{n+1}}}}+\frac{1}{{{S_{n+2}}}}+…+\frac{1}{{{S_{2n}}}}$=$(\frac{1}{n+1}-\frac{1}{n+2})$+$(\frac{1}{n+2}-\frac{1}{n+3})$+…+$(\frac{1}{2n}-\frac{1}{2n+1})]$
=$\frac{1}{n+1}$-$\frac{1}{2n+1}$=$\frac{n}{2{n}^{2}+3n+1}$=$\frac{1}{2n+\frac{1}{n}+3}$≤$\frac{1}{6}$,
∴(cn)max=$\frac{1}{6}$.
∵对任意的正整数n,当m∈[-2,4]时,不等式6t2-12mt+1>6cn恒成立,
∴6t2-12mt+1>1,
化为:t(t-2m)>0,
当m∈(0,4]时,解得t<0,或t>8;
当m=0时,解得t≠0;
当m∈[-2,0)时,解得t<-4,或t>0.
综上可得:t>8,或t<-4.
∴实数t的取值范围是t>8,或t<-4.
点评 本题考查了“裂项求和”、数列的通项公式、不等式的性质,考查了分类讨论方法、变形能力、推理能力与计算能力,属于中档题.

| A. | -2f′(1) | B. | $\frac{1}{2}$f′(1) | C. | -$\frac{1}{2}$f′(1) | D. | f($\frac{1}{2}$) |
| A. | 10π | B. | 12π | C. | 15π | D. | 36π |
| A. | sinα+cosβ=1 | B. | (sinα+cosα)2=1 | C. | sin2α+cos2α=1 | D. | sin2α+cos2β=1 |
 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 ,则不等式
,则不等式 的解集为( )
的解集为( ) B.
B.
 D.(1,2)
D.(1,2) )的图象可看成是把函数y=sin2x的图象作以下平移得到 ( )
)的图象可看成是把函数y=sin2x的图象作以下平移得到 ( )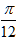 D.向左平移
D.向左平移