题目内容
16.已知在数列{an}中,a1=1,当n≥2时,其前n项和Sn满足Sn2-anSn+2an=0.(1)求数列{an}的通项公式;
(2)若bn=2n-1,记数列{$\frac{1}{{S}_{n}{b}_{n}}$}的前n项和为Tn,求Tn.
分析 (1)把an=Sn-Sn-1代入Sn2-anSn+2an=0整理得出Sn,Sn-1的关系,再由an=Sn-Sn-1得出an.
(2)使用裂项法求出数列的和.
解答 解:(1)∵Sn2-anSn+2an=0,∴Sn2-(Sn-Sn-1)Sn+2(Sn-Sn-1)=0,即SnSn-1+2Sn-2Sn-1=0.
∴$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=$\frac{1}{2}$.∴{$\frac{1}{{S}_{n}}$}是以1为首项,以$\frac{1}{2}$为公差的等差数列.
∴$\frac{1}{{S}_{n}}$=1+$\frac{1}{2}$(n-1)=$\frac{1}{2}$(n+1).∴Sn=$\frac{2}{n+1}$.
∴当n≥2时,an=Sn-Sn-1=$\frac{2}{n+1}$-$\frac{2}{n}$=-$\frac{2}{n(n+1)}$.
∴an=$\left\{\begin{array}{l}{1,n=1}\\{-\frac{2}{n(n+1)},n≥2}\end{array}\right.$.
(2)Tn=1×$\frac{1}{{2}^{0}}$+$\frac{3}{2}$×$\frac{1}{2}$+2×$\frac{1}{{2}^{2}}$+$\frac{5}{2}$×$\frac{1}{{2}^{3}}$+…+$\frac{n+1}{2}$×$\frac{1}{{2}^{n-1}}$,①
∴$\frac{1}{2}$Tn=1×$\frac{1}{2}$+$\frac{3}{2}$×$\frac{1}{{2}^{2}}$+2×$\frac{1}{{2}^{3}}$+$\frac{5}{2}$×$\frac{1}{{2}^{4}}$+…+$\frac{n+1}{2}$×$\frac{1}{{2}^{n}}$,②
①-②得$\frac{1}{2}$Tn=1+$\frac{1}{2}$×$\frac{1}{2}$+$\frac{1}{2}×$$\frac{1}{{2}^{2}}$+$\frac{1}{2}×$$\frac{1}{{2}^{3}}$+…+$\frac{1}{2}×$$\frac{1}{{2}^{n-1}}$-$\frac{n+1}{{2}^{n+1}}$=1+$\frac{1}{2}$($\frac{\frac{1}{2}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}$)-$\frac{n+1}{{2}^{n+1}}$=$\frac{3}{2}$-$\frac{1}{{2}^{n}}$-$\frac{n+1}{{2}^{n+1}}$=$\frac{3}{2}$-$\frac{n+3}{{2}^{n+1}}$.
∴Tn=3-$\frac{n+3}{{2}^{n}}$.
点评 本题考查了数列通项公式的求法,裂项法求和,发现{$\frac{1}{{S}_{n}}$}是等差数列是解题关键,属于难题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
| A. | 8 | B. | $4\sqrt{2}$ | C. | 4 | D. | $2\sqrt{2}$ |
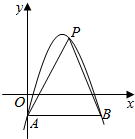 姐图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B,点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.
姐图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B,点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.