题目内容
7.函数f(x)=-x2+bx+c,f(0)=f(2)=1,则f(-2)=-7.分析 根据函数的对称性,求出b,根据f(0)=0,求出c,从而求出f(x)的表达式,求出f(-2)的值即可.
解答 解:f(x)=-x2+bx+c,
f(0)=f(2)=1,
对称轴x=$-\frac{b}{-2}$=1,解得:b=2,
而f(0)=c=1,
∴f(x)=-x2+2x+1,
∴f(-2)=-4-4+1=-7,
故答案为:-7.
点评 本题考查了二次函数的性质,考查求函数的表达式,求函数值问题,是一道基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
17.使arccos(1-x)有意义的x的取值范围是( )
| A. | [1-π,1] | B. | [0,2] | C. | (-∞,1] | D. | [-1,1] |
 如图,AB是圆的直径,C是圆上的点,且PA⊥BC.
如图,AB是圆的直径,C是圆上的点,且PA⊥BC.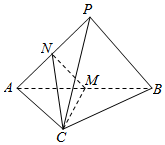 如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA⊥PB,M,N分别为AB,PA的中点.
如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA⊥PB,M,N分别为AB,PA的中点.