题目内容
7.已知$\frac{1}{cosα}$和tanα是方程x2+3x+m=0的两根,试求实数m的值.分析 利用由韦达定理,$\frac{1}{cosα}+tanα=-3$,切化弦即$\frac{1+sinα}{cosα}=-3$,利用三角变换求解即可.
解答 解:由韦达定理,$\frac{1}{cosα}+tanα=-3$,即$\frac{1+sinα}{cosα}=-3$,
两边平方并整理得5sin2α+sinα-4=0
∴$sinα=\frac{4}{5}$或-1(不合题意,舍),
于是,$m=\frac{1}{cosα}•tanα=\frac{sinα}{{{{cos}^2}α}}=\frac{sinα}{{1-{{sin}^2}α}}=\frac{20}{9}$,
点评 本题考查方程的根与系数的关系,三角变换的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.若直线l1:(2m+1)x-4y+3m=0与直线l2:x+(m+5)y-3m=0平行,则m的值为( )
| A. | $-\frac{9}{2}或-1$ | B. | $-\frac{9}{2}$ | C. | $-\frac{19}{2}$ | D. | -1 |
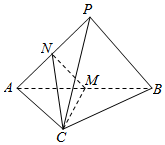 如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA⊥PB,M,N分别为AB,PA的中点.
如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA⊥PB,M,N分别为AB,PA的中点.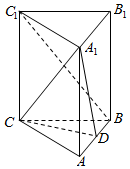 在三棱柱ABC-A1B1C1中,底面三角形ABC是等边三角形,侧棱AA1⊥底面ABC,D为棱AB的中点
在三棱柱ABC-A1B1C1中,底面三角形ABC是等边三角形,侧棱AA1⊥底面ABC,D为棱AB的中点