题目内容
已知双曲线C:
-
=1(a>0,b>0)的离心率为
,左、右焦点分别为F1、F2,一条准线的方程为x=
.
(1)求双曲线C的方程;
(2)若双曲线C上的一点P满足
•
=1,求|
|•|
|的值.
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
| 3 |
| 2 |
(1)求双曲线C的方程;
(2)若双曲线C上的一点P满足
| PF1 |
| PF2 |
| PF1 |
| PF2 |
考点:轨迹方程,平面向量数量积的运算
专题:计算题,平面向量及应用,圆锥曲线的定义、性质与方程
分析:(1)运用双曲线的准线方程和离心率公式,得到方程组,解出即可得到双曲线方程;
(2)设|
|=r1, |
|=r2, ∠F1PF2=θ.运用向量的数量积的定义,结合双曲线的定义和余弦定理,化简即可得到.
(2)设|
| PF1 |
| PF2 |
解答:
解:(1)由条件有
,∴
∴a2=3,b2=c2-a2=1.
故双曲线C的方程为:
-y2=1;
(2)设|
|=r1, |
|=r2, ∠F1PF2=θ.
∵
•
=1∴r1•r2•cosθ=1,
又|r1-r2|=2
∴
+
-2r1r2=12,即
+
=2r1r2+12.
又由余弦定理有:4c2=
+
-2r1r2cosθ.
即16=2r1r2+12-2,∴r1r2=3.
故|
|•|
|=3.
|
|
∴a2=3,b2=c2-a2=1.
故双曲线C的方程为:
| x2 |
| 3 |
(2)设|
| PF1 |
| PF2 |
∵
| PF1 |
| PF2 |
又|r1-r2|=2
| 3 |
| r | 2 1 |
| r | 2 2 |
| r | 2 1 |
| r | 2 2 |
又由余弦定理有:4c2=
| r | 2 1 |
| r | 2 2 |
即16=2r1r2+12-2,∴r1r2=3.
故|
| PF1 |
| PF2 |
点评:本题考查双曲线的定义、方程和性质,考查平面向量的数量积的定义和余弦定理及运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
已知两条相交直线a、b,a∥平面α,则b与平面α的位置关系( )
| A、b∥α |
| B、b与α相交 |
| C、b?α |
| D、b∥α或b与α相交 |
设M(x,y)是区域
内的动点,且不等式x+2y≤14恒成立,则实数a的取值范围是( )
|
| A、[8,10] |
| B、[8,9] |
| C、[6,9] |
| D、[6,10] |
函数f(x)=sin(-2x)的一个单调增区间是( )
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
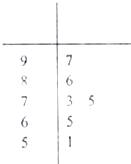 某校高一级数学必修一模块考试的成绩分为四个等级,85分-100分为A等,70分-84分为B等,55分-69分为C等,54分以下为D等.右边的茎叶图(十位为茎,个位为叶)记录了某班某小组6名学生的数学必修一模块考试成绩.
某校高一级数学必修一模块考试的成绩分为四个等级,85分-100分为A等,70分-84分为B等,55分-69分为C等,54分以下为D等.右边的茎叶图(十位为茎,个位为叶)记录了某班某小组6名学生的数学必修一模块考试成绩.