题目内容
(本小题满分11分)已知函数 ,其中
,其中 ,且曲线
,且曲线 在点
在点 的
的
切线垂直于直线 .
.
(Ⅰ)求 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数 的单调区间和极值.
的单调区间和极值.
(Ⅰ)-2 (Ⅱ) 在
在 内为减函数,在
内为减函数,在 内为增函数,
内为增函数, 在
在 处取得极小值
处取得极小值 ,无极大值.
,无极大值.
【解析】
试题分析:对于第一问,根据两直线垂直,可以得出切线的斜率,从而得出函数在某个点处的导数,从而得出 所满足的条件,从而求出
所满足的条件,从而求出 的值,对于第二问,函数的单调区间和函数的极值,把握住导数的应用即可.
的值,对于第二问,函数的单调区间和函数的极值,把握住导数的应用即可.
试题解析:(Ⅰ) 2分
2分
∵曲线 在点
在点 处的切线垂直于直线
处的切线垂直于直线
∴ ,∴
,∴ 4分
4分
(Ⅱ)由(Ⅰ)知 ,则
,则
令 ,解得
,解得 , 又
, 又 的定义域为
的定义域为 6分
6分
当 时,
时, ∴
∴ 在
在 内为减函数 8分
内为减函数 8分
当 时,
时, ∴
∴ 在
在 内为增函数 10分
内为增函数 10分
由此知函数 在
在 处取得极小值
处取得极小值 ,无极大值。 11分
,无极大值。 11分
考点:导数的几何意义,导数的应用.

练习册系列答案
相关题目
从某项综合能力测试中抽取50人的成绩,统计如下表,则这50人成绩的平
均数为__________,方差为__________.
| 分数 | 5 | 4 | 3 | 2 | 1 |
| 人数 | 10 | 5 | 15 | 15 | 5 |
(注:s2=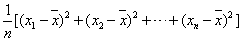 ,
,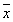 为数据
为数据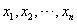 的平均数)
的平均数)
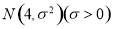 ,若X在(0,8)内取值的概率为0.6,则X在(0,4)内取值的概率为
,若X在(0,8)内取值的概率为0.6,则X在(0,4)内取值的概率为
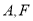 分别是椭圆
分别是椭圆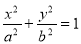
 的上顶点和右焦点,直线
的上顶点和右焦点,直线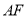 与椭圆交于另一点
与椭圆交于另一点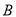 ,过中心
,过中心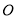 作直线
作直线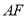 的平行线交椭圆于
的平行线交椭圆于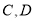 两点,若
两点,若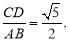 则椭圆的离心率为 .
则椭圆的离心率为 .
 中,各项都是正数,且
中,各项都是正数,且 成等差数列,则
成等差数列,则 等于 .
等于 . 为第三项,3为第六项的等比数列的公比,则
为第三项,3为第六项的等比数列的公比,则 ________.
________. 的离心率等于( )
的离心率等于( ) B.
B. C.
C. 

