题目内容
(本小题满分12分)如图, 为正三角形,
为正三角形, 平面
平面 ,
, ,
, 为
为 的中点,
的中点, ,
, .
.

(Ⅰ)求证:
 平面
平面 ;
;
(Ⅱ)求平面 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(Ⅰ)见解析;(Ⅱ)
【解析】
试题分析:(Ⅰ)作 的中点
的中点 ,只需证明
,只需证明 即可;(Ⅱ)可以建立坐标系,利用法向量求解,也可以证明平面
即可;(Ⅱ)可以建立坐标系,利用法向量求解,也可以证明平面 与平面
与平面 所成的锐二面角就是∠EAC,再计算即可.
所成的锐二面角就是∠EAC,再计算即可.
试题解析:(Ⅰ)证明:作 的中点
的中点 ,连结
,连结 .
.
在 中,
中,
 ,又据题意知,
,又据题意知,
 .
.
∴
 ,∴四边形
,∴四边形 为平行四边形.
为平行四边形.
∴ ,又
,又 平面
平面 ,
, 平面
平面 .
.
∴ 平面
平面 . 4分
. 4分
(Ⅱ)∵
 ,∴
,∴ 平面
平面 .
.
在正 中,
中, ,∴
,∴ 三线两两垂直.
三线两两垂直.
分别以 为
为 轴,建系如图.
轴,建系如图.

则 ,
, ,
, .
.
∴ ,
, .
.
设平面 的一个法向量为
的一个法向量为 ,
,
则 ,即
,即 ,令
,令 ,则
,则 .
.
∴平面 的一个法向量为
的一个法向量为 .
.
又平面 的一个法向量为
的一个法向量为 .
.
∴ .
.
∴平面 与平面
与平面 所成的锐二面角的余弦值
所成的锐二面角的余弦值 . 8分
. 8分
考点:空间线面关系,二面角

练习册系列答案
相关题目
 的坐标为( )
的坐标为( )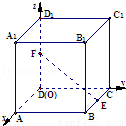
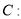
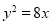 ,过点
,过点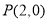 的直线与抛物线交于
的直线与抛物线交于 ,
,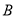 两点,
两点,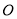 为坐标原点,则
为坐标原点,则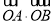 的值为
的值为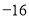 (B)
(B)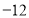 (C)
(C)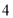 (D)
(D)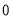
 ,集合
,集合 ,则
,则 ( )
( ) (B)
(B)
 (D)
(D)
 的展开式中含
的展开式中含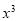 的项的系数是__________.(用数字作答)
的项的系数是__________.(用数字作答)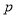 :“若
:“若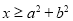 ,则
,则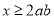 ”,则下列说法正确的是( )
”,则下列说法正确的是( ) ,则
,则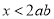 ”
” 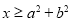 ,则
,则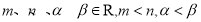 ,若
,若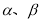 是函数
是函数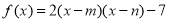 的零点,则
的零点,则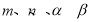 四个数按从小到大的顺序是 (用符号
四个数按从小到大的顺序是 (用符号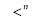 连接起来).
连接起来). 的重心为G,角A,B,C所对的边分别为
的重心为G,角A,B,C所对的边分别为 ,若
,若 ,则
,则
 C.
C. D.
D.