题目内容
若不等式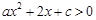 和
和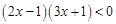 有相同的解集,则不等
有相同的解集,则不等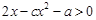 的解集是 ( )
的解集是 ( )
A. | B.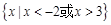 |
C.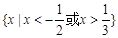 | D.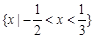 |
A
解析试题分析:因为不等式 ,因此可知不等式
,因此可知不等式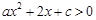 的解集为
的解集为 ,那么结合韦达定理可知,
,那么结合韦达定理可知, ,解得a=-3,c=
,解得a=-3,c= ,因此不等式
,因此不等式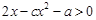 即为
即为 ,那么结合二次函数的性质和不等式的求解得到结论为
,那么结合二次函数的性质和不等式的求解得到结论为 ,选A.
,选A.
考点:本题主要考查了一元二次不等式的解集的运用。
点评:解决该试题的关键是能利用解集相同得到方程的根,结合韦达定理得到系数a,,c的值,进而求解不等式的解集。

练习册系列答案
相关题目
设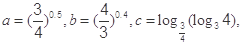 则( ).
则( ).
A.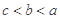 | B.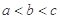 | C.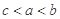 | D.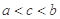 |
若不等式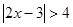 与不等式
与不等式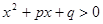 的解集相同,则p:q等于 ( )
的解集相同,则p:q等于 ( )
| A.12:7 | B.7:12 | C.-12:7 | D.-3 :4 |
对任意的实数 ,不等式
,不等式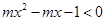 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是
A.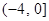 | B.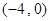 | C.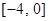 | D.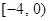 |
在R上定义运算 若不等式
若不等式 对任意实数
对任意实数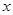 成立,则( )
成立,则( )
A. | B.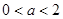 |
C.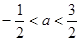 | D.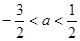 |
不等式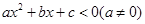 的解集为
的解集为 ,那么( )
,那么( )
A.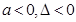 | B.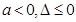 | C.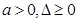 | D.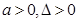 |
设不等式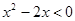 的解集为M,函数
的解集为M,函数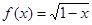 的定义域为N,则
的定义域为N,则 为( )
为( )
| A.(0,1) | B.(0,2) | C.(0,1] | D.(0,2] |
若2-m与|m|-3同号,则m的取值范围是 ( )
| A.(3,+∞) | B.(-3,3) |
| C.(2,3)∪(-∞,-3) | D.(-3,2)∪(3,+∞) |
不等式 对任意实数
对任意实数 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
A. | B. ( ( | C. | D. |