题目内容
设不等式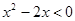 的解集为M,函数
的解集为M,函数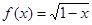 的定义域为N,则
的定义域为N,则 为( )
为( )
| A.(0,1) | B.(0,2) | C.(0,1] | D.(0,2] |
C
解析试题分析: 由于不等式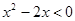 等价于x(x-2)<0,解得0<x<2,故集合M={x|0<x<2}
等价于x(x-2)<0,解得0<x<2,故集合M={x|0<x<2}
而作为函数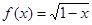 的定义域为,偶次根式下被开方数为非负数,则满足,1-x
的定义域为,偶次根式下被开方数为非负数,则满足,1-x 故集合N={x|x
故集合N={x|x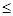 1},因此通过集合的交集的运算可知,
1},因此通过集合的交集的运算可知,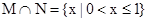 选C.
选C.
考点:本题主要考查了函数的定义域和一元二次不等式的求解。
点评:解决该试题的关键是准确的翻译出集合M,N,然后运用集合的交集的运算,得到结论。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果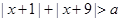 对任意实数x总成立,则a的取值范围是 ( )
对任意实数x总成立,则a的取值范围是 ( )
A. | B. | C. | D.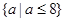 |
若不等式 成立的充分条件是
成立的充分条件是 ,则实数
,则实数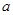 的取值范围是( )
的取值范围是( )
A.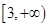 | B. | C. | D.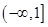 |
若不等式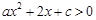 和
和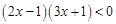 有相同的解集,则不等
有相同的解集,则不等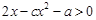 的解集是 ( )
的解集是 ( )
A. | B.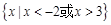 |
C.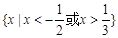 | D.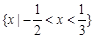 |
不等式 对于
对于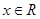 恒成立,那么
恒成立,那么 的取值范围是( )
的取值范围是( )
A. | B.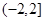 | C. | D. |
不等式 的解集是
的解集是
A. | B. |
C. | D. 或 或 或 或 |
设xy<0,x,y∈R,那么下列结论正确的是( )
| A.|x+y|<|x-y| | B.|x-y|<|x|+|y| |
| C.|x+y|>|x-y| | D.|x-y|<||x|-|y|| |
若关于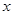 的不等式
的不等式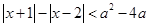 有实数解,则实数
有实数解,则实数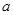 的取值范围为( )
的取值范围为( )
A.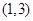 | B. | C.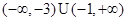 | D. |
 的解集为( )
的解集为( )






