题目内容
对任意的实数 ,不等式
,不等式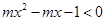 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是
A.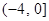 | B.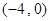 | C.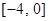 | D.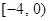 |
A
解析试题分析:当m=0时,mx2-mx-1=-1<0,不等式成立;
设y=mx2-mx-1,当m≠0时函数y为二次函数,y要恒小于0,抛物线开口向下且与x轴没有交点,即要m<0且△<0
得到:m<0,△=m2+4m<0解得-4<m<0.
综上得到-4<m≤0.
故选A.
考点:本题以不等式恒成立为平台,考查学生会求一元二次不等式的解集.同时要求学生把二次函数的图象性质与一元二次不等式结合起来解决数学问题。
点评:解决该试题的关键是当m=0时,不等式显然成立;当m≠0时,根据二次函数图象的性质得到m的取值范围.两者取并集即可得到m的取值范围.用分类讨论思想得到。

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
若不等式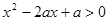 ,对
,对 恒成立,则关于
恒成立,则关于 的不等式
的不等式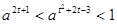 的解集为( )
的解集为( )
A. | B. | C. | D.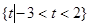 |
不等式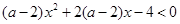 对一切
对一切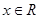 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )
A.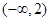 | B.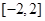 | C.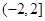 | D.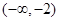 |
当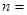 1,2,3,4,5,6时,比较
1,2,3,4,5,6时,比较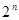 和
和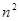 的大小并猜想( )
的大小并猜想( )
A.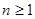 时, 时,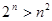 | B.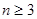 时, 时,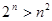 |
C.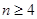 时, 时,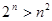 | D.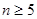 时, 时,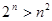 |
若不等式 成立的充分条件是
成立的充分条件是 ,则实数
,则实数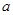 的取值范围是( )
的取值范围是( )
A.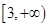 | B. | C. | D.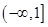 |
不等式 的解集为R,则
的解集为R,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
若不等式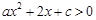 和
和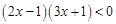 有相同的解集,则不等
有相同的解集,则不等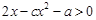 的解集是 ( )
的解集是 ( )
A. | B.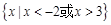 |
C.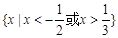 | D.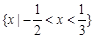 |
不等式 的解集是
的解集是
A. | B. |
C. | D. 或 或 或 或 |
不等式 的解集非空的一个必要而不充分条件是( )
的解集非空的一个必要而不充分条件是( )
A. | B. | C. | D. |