题目内容
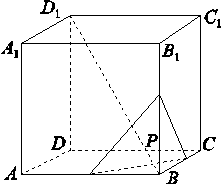
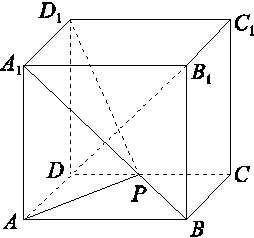
如图,正方体ABCD-A1B1C1D1的棱长为2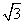 ,动点P在对角线BD1上,过点P作垂直于BD1的平面α,记这样得到的截面多边形(含三角形)的周长为y,设BP=x,则当x∈[1,5]时,函数y=f(x)的值域为( )
,动点P在对角线BD1上,过点P作垂直于BD1的平面α,记这样得到的截面多边形(含三角形)的周长为y,设BP=x,则当x∈[1,5]时,函数y=f(x)的值域为( )
A.[2 ,6
,6 ] B.[2
] B.[2 ,18]
,18]
C.[3 ,18] D.[3
,18] D.[3 ,6
,6 ]
]
D
[解析] 当点P从点B向D1运动时,截面的周长y越来越大,当截面经过平面AB1C时,周长最大,当点P继续移动时,在截面AB1C到截面A1DC1之间,截面周长不变,当点P继续移动时,截面周长越来越小,所以截面周长的最大值就是△AB1C的周长.因为正方体的棱长为2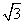 ,所以AC=2
,所以AC=2 ,即周长为6
,即周长为6 .当x=1时,截面的周长最小,如图,
.当x=1时,截面的周长最小,如图,

设△EFG的边长为 ,BF2+BE2=EF2=
,BF2+BE2=EF2= ,又BF=BE,所以BE=
,又BF=BE,所以BE= ,连接EP交FG于点M,连接BM,因为P是等边三角形EFG的中心,所以FM=
,连接EP交FG于点M,连接BM,因为P是等边三角形EFG的中心,所以FM= ,所以EM2=EF2-FM2=
,所以EM2=EF2-FM2= 2,因为EP=
2,因为EP= EM,所以EP=
EM,所以EP=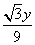 .又BP2+EP2=BE2,即12+
.又BP2+EP2=BE2,即12+ ,得y=3
,得y=3 ,所以值域为[3
,所以值域为[3 ,6
,6 ](或由平面AB1C∥平面FEG,BP=1可知E,F,G分别是BB1,AB,BC的中点,则△EFG的周长为△AB1C的一半,即3
](或由平面AB1C∥平面FEG,BP=1可知E,F,G分别是BB1,AB,BC的中点,则△EFG的周长为△AB1C的一半,即3 ).
).

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
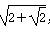
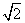 ,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.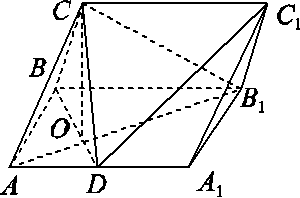
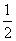 x+a,则函数f(x)的零点个数是( )
x+a,则函数f(x)的零点个数是( ) 若存在k使得函数f(x)的值域是[0,2],则实数a的取值范围是( )
若存在k使得函数f(x)的值域是[0,2],则实数a的取值范围是( )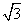 ,+∞) B.
,+∞) B.