Question

已知在四边形ABCD中，AD∥BC，AD=AB=1，∠BCD=45°,∠BAD=90°,将△ABD沿对角线BD折起到如下图所示PBD的位置，使平面PBD⊥平面BCD.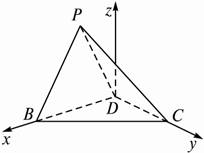

(1)求证：CD⊥PB；

（2）求二面角P—BC—D的大小（用反三角函数表示）；

（3）求点D到平面PBC的距离.

Answer 1

解析：∵∠BAD=90°,AD=AB,?

∴∠ADB=∠ABD=45°.∵AD∥BC,∠BCD=45°,∴∠BDC=90°,∴BD⊥DC.?

如下图所示建立空间直角坐标系D—xyz,设BA=1，?

则D（0，0，0），B（2，0，0），C（0，2，0），P（，0，）.

(1)证明：=(0,- ,0),=(,0,- ).?

∴·=0，?

∴⊥,∴CD⊥PB.

(2)解：取平面BDC的法向量n=(0,0,1),?

设平面PBC的法向量为m=(x,y,z)?

∵=(,0,- ),=(-,,- ),?

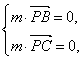∴即

令x=z=1,∴y=1,∴m=(1,1,1).?

∴cos〈n,m〉===.?

∴二面角P—BC—D的大小为arccos.

(3)解：过D做DM⊥平面PBC于点M，?

∴cos〈,m〉==.?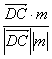

∴D到平面PBC的距离||=||×cos〈,m〉=.