题目内容
已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为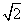 ,且过点(4,-
,且过点(4,-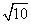 ).点M(3,m)在双曲线上.
).点M(3,m)在双曲线上.
(1)求双曲线方程;
(2)求证: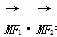 =0;
=0;
(3)求△F1MF2面积.
解:(1)∵e=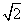 ,∴可设双曲线方程为x2-y2=λ.
,∴可设双曲线方程为x2-y2=λ.
∵过点(4,-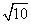 ),∴16-10=λ,即λ=6.
),∴16-10=λ,即λ=6.
∴双曲线方程为x2-y2=6.
(2)证明:由(1)可知,双曲线中a=b= ,
,
∴c=2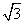 ,
,
∴F1(-2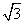 ,0),F2(2
,0),F2(2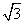 ,0),
,0),
∵ =(-3-2
=(-3-2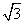 ,-m),
,-m), =(2
=(2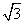 -3,-m),
-3,-m),
∴ =(3+2
=(3+2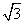 )×(3-2
)×(3-2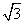 )+m2
)+m2
=-3+m2,
∵M点在双曲线上,∴9-m2=6,即m2-3=0,
 (3)△F1MF2的底|F1F2|=4
(3)△F1MF2的底|F1F2|=4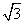 ,由(2)知m=±
,由(2)知m=±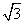 .
.
∴△F1MF2的高h=|m|=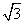 ,∴S△F1MF2=6.
,∴S△F1MF2=6.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 +y2=1的左、右焦点.
+y2=1的左、右焦点. =-
=- ,求点P的坐标;
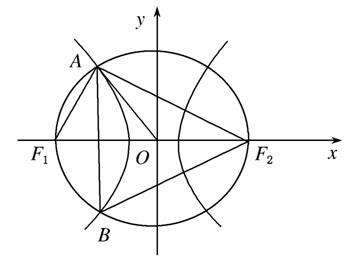
,求点P的坐标;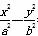 =1(a>0,b>0)的两个焦点,以坐标原点O为圆心,|OF1|为半径的圆与该双曲线的左支的两个交点分别为A,B,且△F2AB是等边三角形,则双曲线的离心率为( )
=1(a>0,b>0)的两个焦点,以坐标原点O为圆心,|OF1|为半径的圆与该双曲线的左支的两个交点分别为A,B,且△F2AB是等边三角形,则双曲线的离心率为( )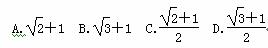

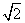 ),且与直线l相切,椭圆N的对称轴为坐标轴,一个焦点是F,点A(1,
),且与直线l相切,椭圆N的对称轴为坐标轴,一个焦点是F,点A(1,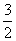 的直线l是否存在?若存在,请求出直线l的方程;若不存在,请说明理由.
的直线l是否存在?若存在,请求出直线l的方程;若不存在,请说明理由.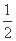 (C)-
(C)-