题目内容
已知动圆P过定点F(0,-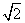 ),且与直线l相切,椭圆N的对称轴为坐标轴,一个焦点是F,点A(1,
),且与直线l相切,椭圆N的对称轴为坐标轴,一个焦点是F,点A(1,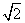 )在椭圆N上.
)在椭圆N上.
(1)求动圆圆心P的轨迹M的方程和椭圆N的方程;
(2)已知与轨迹M在x=-4处的切线平行的直线与椭圆N交于B、C两点,试探求使△ABC面积等于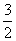 的直线l是否存在?若存在,请求出直线l的方程;若不存在,请说明理由.
的直线l是否存在?若存在,请求出直线l的方程;若不存在,请说明理由.
解:(1)由题意知:点P到定点F(0,-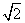 )和直线y=
)和直线y=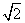 的距离相等,故P的轨迹M是以F为焦点,y=
的距离相等,故P的轨迹M是以F为焦点,y=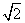 为准线的抛物线.
为准线的抛物线.
∴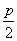 =
=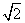 ,∴p=2
,∴p=2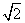
∴轨迹M的方程为:x2=-4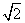 y
y
又由题意:可设椭圆方程为: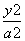 +
+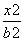 =1(a>b>0)
=1(a>b>0)
∴2a= =4
=4
∴a=2,又c=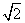 ,∴b=
,∴b=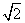 ,
,
∴椭圆N的方程为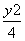 +
+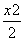 =1.
=1.
(2)不存在满足条件的直线l.
理由如下:若存在这样的直线l,
∵轨迹M为抛物线x2=-4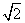 y,它在x=-4处的切线斜率为k=
y,它在x=-4处的切线斜率为k=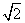 .
.
故可设l的方程为:y=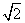 x+m,
x+m,
联立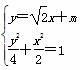 消去y整理得,4x2+2
消去y整理得,4x2+2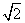 mx+m2-4=0
mx+m2-4=0
∴Δ=(2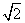 m)2-16(m2-4)>0,∴m2<8且m≠0,
m)2-16(m2-4)>0,∴m2<8且m≠0,
设B(x1,y1),C(x2,y2),则x1+x2=-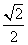 m,x1x2=
m,x1x2=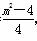 ,
,
由两点间的距离公式可求得|BC|=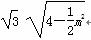
又点A到l距离d=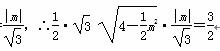 ∴m4-8m2+18=0,显然此方程无解,即m不存在,
∴m4-8m2+18=0,显然此方程无解,即m不存在,
故这样的直线l不存在.

练习册系列答案
相关题目
 x2的焦点.直线4x-3y-3=0与圆C相交于A,B两点,且|AB|=8,则圆C的方程为________.
x2的焦点.直线4x-3y-3=0与圆C相交于A,B两点,且|AB|=8,则圆C的方程为________.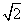 ,且过点(4,-
,且过点(4,-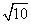 ).点M(3,m)在双曲线上.
).点M(3,m)在双曲线上.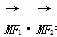 =0;
=0;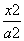 +
+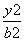 =1(a>b>0)与双曲线
=1(a>b>0)与双曲线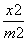 -
-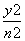 =1(m>0,n>0)有相同的焦点(-c,0)和(c,0),若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是( )
=1(m>0,n>0)有相同的焦点(-c,0)和(c,0),若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是( )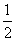 B.
B.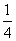 C.
C. D.
D.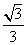
 的最小值.
的最小值. )2an(n∈N*),则数列{an}的通项公式为 .
)2an(n∈N*),则数列{an}的通项公式为 .