题目内容
函数f（x）=5
cos2x+
sin2x-4sinxcosx
（1）求f（
）
（2）若f（α）=5
，α∈（
，π），求角α．
| 3 |
| 3 |
（1）求f（
| 5π |
| 12 |
（2）若f（α）=5
| 3 |
| π |
| 2 |
考点：三角函数中的恒等变换应用,函数的值
专题：三角函数的求值,三角函数的图像与性质
分析：（1）首先通过三角恒等变换把三角函数的关系式变形成余弦型函数，进一步求出函数的值．
（2）利用（1）的结论，建立关于α的三角方程，通过解三角方程求出角α的值．
（2）利用（1）的结论，建立关于α的三角方程，通过解三角方程求出角α的值．
解答：
解：（1）f（x）=5
cos2x+
sin2x-4sinxcosx
=5
cos2x+
(1-cos2x)-2sin2x
=4
cos2x-2sin2x+
=4
-2sin2x+
=2
cos2x-2sin2x+3
=4cos(2x+
)+3
所以：f(
)=4cos(
+
)+3
=3
-4
（2）由（1）得：f（x）=4cos(2x+
)+3
则：f(α)=4cos(2α+
)+3
=5
所以：4cos(2α+
)=2
进一步求得：cos(2α+
)=
又α∈（
，π），
所以：2α+
=2kπ±
（k∈Z）
解得：当k=1时，α=
| 3 |
| 3 |
=5
| 3 |
| 3 |
=4
| 3 |
| 3 |
=4
| 3 |
| cos2x+1 |
| 2 |
| 3 |
=2
| 3 |
| 3 |
=4cos(2x+
| π |
| 6 |
| 3 |
所以：f(
| 5π |
| 12 |
| 10π |
| 12 |
| π |
| 6 |
| 3 |
| 3 |
（2）由（1）得：f（x）=4cos(2x+
| π |
| 6 |
| 3 |
则：f(α)=4cos(2α+
| π |
| 6 |
| 3 |
| 3 |
所以：4cos(2α+
| π |
| 6 |
| 3 |
进一步求得：cos(2α+
| π |
| 6 |
| ||
| 2 |
又α∈（
| π |
| 2 |
所以：2α+
| π |
| 6 |
| π |
| 6 |
解得：当k=1时，α=
| 5π |
| 6 |
点评：本题考查的知识要点：三角函数关系式的恒等变换，及三角方程的解法，属于基础题型．
练习册系列答案
相关题目
如图，网格纸上小方格的边长为1（表示1cm），图中粗线和虚线是某零件的三视图，该零件是由一个底面半径为4cm，高为3cm的圆锥毛坯切割得到，则毛坯表面积与切削得的零件表面积的比值为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知抛物线y2=2px（p＞0）上一点M（1，m）（m＞0）到其焦点的距离为5，双曲线
-y2=1的左顶点为A，若双曲线的一条渐近线与直线AM平行，则实数a的值是（ ）
| x2 |
| a |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知
，
满足|
|=5，|
|≤1，且|
-4
|≤
，则
•
的最小值为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| 21 |
| a |
| b |
A、
| ||||
| B、-5 | ||||
C、
| ||||
D、-
|
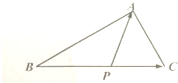如图，已知△ABC中，A=90°，B=30°，点P在BC上运动且满足| CP |
| CB |
| PA |
| PC |
A、
| ||
B、
| ||
C、
| ||
D、
|