题目内容
若log2a
<0,则a的取值范围是______.
| 1+a2 |
| 1+a |
根据对数函数的性质,分两种情况,
①、0<2a<1,即0<a<
时,y=log2ax为减函数,
若log2a
<0,有
>1,
解可得,a>1,
又有0<a<
,故符合条件的a不存在;
②、2a>1,即a>
时,
若log2a
<0,有0<
<1,
解可得,0<a<1,
又有a>
,故符合条件的a范围为
<a<1,
综合可得,a的取值范围是
<a<1.
①、0<2a<1,即0<a<
| 1 |
| 2 |
若log2a
| 1+a2 |
| 1+a |
| 1+a2 |
| 1+a |
解可得,a>1,
又有0<a<
| 1 |
| 2 |
②、2a>1,即a>
| 1 |
| 2 |
若log2a
| 1+a2 |
| 1+a |
| 1+a2 |
| 1+a |
解可得,0<a<1,
又有a>
| 1 |
| 2 |
| 1 |
| 2 |
综合可得,a的取值范围是
| 1 |
| 2 |

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 恒成立,求实数M的最小值.
恒成立,求实数M的最小值. 恒成立,求实数M的最小值.
恒成立,求实数M的最小值.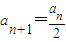 ;当an为奇数时,
;当an为奇数时,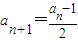 .
.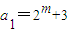 (m>3且m∈N),数列{an}的前n项和为Sn,求证:
(m>3且m∈N),数列{an}的前n项和为Sn,求证: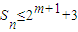 ;
;