题目内容
18．
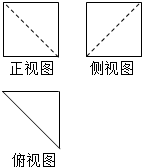如图是一个多面体的三视图，其中正视图为正方形，俯视图是腰长为2的等腰直角三角形，则该多面体的最大面的面积是4$\sqrt{2}$．
分析 利用三视图复原的几何体的形状，通过三视图的数据求出该几何体的最大面的面积．
解答 解：由题意知，三视图复原的几何体如图所示：
四棱锥S-BCDE，是正方体的一部分，正方体的棱长为2；
所以几何体的最大面为矩形BCDE，
它的面积为2×2$\sqrt{2}$=4$\sqrt{2}$．
故答案为：4$\sqrt{2}$．
点评 本题考查三视图与几何体的直观图的关系，判断三视图复原的几何体的形状是解题的关键．
练习册系列答案
相关题目
8．已知Sn为数列{an}的前n项和，且a1=$\frac{1}{2}$，an+1=1-$\frac{1}{{a}_{n}}$，则S10=（ ）
| A． | 4 | B． | $\frac{9}{2}$ | C． | 5 | D． | 6 |
14．对某产品1至6月份销售量及其价格进行调查，其售价x和销售量y之间的一组数据如下表所示：
（Ⅰ）根据1至5月份的数据，求出y关于x的回归直线方程；
（Ⅱ）若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元，则认为所得到的回归直线方程是理想的，试问所得回归直线方程是否理想？
（Ⅲ）预计在今后的销售中，销售量与单价仍然服从（Ⅰ）中的关系，且该产品的成本是2.5元/件，为获得最大利润，该产品的单价应定为多少元？（利润=销售收入-成本）．
参考公式：回归方程$\hat y=\hat bx+\hat a$，其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$．参考数据：$\sum_{i=1}^5{{x_i}{y_i}=392}$，$\sum_{i=1}^5{x_i^2}=502.5$．
| 月份i | 1 | 2 | 3 | 4 | 5 | 6 |
| 单价xi（元） | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
| 销售量yi（件） | 11 | 10 | 8 | 6 | 5 | 14 |
（Ⅱ）若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元，则认为所得到的回归直线方程是理想的，试问所得回归直线方程是否理想？
（Ⅲ）预计在今后的销售中，销售量与单价仍然服从（Ⅰ）中的关系，且该产品的成本是2.5元/件，为获得最大利润，该产品的单价应定为多少元？（利润=销售收入-成本）．
参考公式：回归方程$\hat y=\hat bx+\hat a$，其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$．参考数据：$\sum_{i=1}^5{{x_i}{y_i}=392}$，$\sum_{i=1}^5{x_i^2}=502.5$．