题目内容
8.已知Sn为数列{an}的前n项和,且a1=$\frac{1}{2}$,an+1=1-$\frac{1}{{a}_{n}}$,则S10=( )| A. | 4 | B. | $\frac{9}{2}$ | C. | 5 | D. | 6 |
分析 由a1=$\frac{1}{2}$,an+1=1-$\frac{1}{{a}_{n}}$,可得:a2=-1,a3=2,a4=$\frac{1}{2}$,…,an+3=an.即可得出.
解答 解:∵a1=$\frac{1}{2}$,an+1=1-$\frac{1}{{a}_{n}}$,
∴a2=1-$\frac{1}{\frac{1}{2}}$=-1,同理可得:a3=2,a4=$\frac{1}{2}$,…,
∴an+3=an.
∵a1+a2+a3=$\frac{1}{2}-1+2$=$\frac{3}{2}$.
则S10=$\frac{3}{2}×3$+$\frac{1}{2}$=5.
故选:C.
点评 本题考查了递推公式、数列的周期性,考查了推理能力与计算能力,属于中档.

练习册系列答案
相关题目
18.设命题p:存在四边相等的四边形不是正方形;命题q:若cosx=cosy,则x=y,则下列判断正确的是( )
| A. | p∧q为真 | B. | p∨q为假 | C. | ¬p为真 | D. | ¬q为真 |
19.函数f(x)=$\sqrt{2-{2}^{x}}$+$\frac{1}{lo{g}_{3}x}$的定义域为( )
| A. | {x|x<1} | B. | {x|0<x<1} | C. | {x|0<x≤1} | D. | {x|x>1} |
3.函数f(x)=sinx(sinx+$\sqrt{3}$cosx)的最大值为 ( )
| A. | 2 | B. | 1+$\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | 1 |
13.已知△ABC是边长为1的等边三角形,则($\overrightarrow{AB}$-2$\overrightarrow{BC}$)(3$\overrightarrow{BC}$+4$\overrightarrow{CA}$)=( )
| A. | $-\frac{13}{2}$ | B. | $-\frac{11}{2}$ | C. | $-6-\frac{{\sqrt{3}}}{2}$ | D. | $-6+\frac{{\sqrt{3}}}{2}$ |
20.直线x-y+4=0被圆(x+2)2+(y-2)2=2截得的弦长等于( )
| A. | $12\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | $4\sqrt{2}$ |
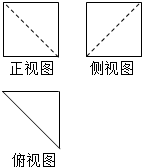 如图是一个多面体的三视图,其中正视图为正方形,俯视图是腰长为2的等腰直角三角形,则该多面体的最大面的面积是4$\sqrt{2}$.
如图是一个多面体的三视图,其中正视图为正方形,俯视图是腰长为2的等腰直角三角形,则该多面体的最大面的面积是4$\sqrt{2}$.