题目内容
13.下列命题正确的是(2)(5)(1)若$\overrightarrow{a}$≠$\overrightarrow{o}$,$\overrightarrow{a}•\overrightarrow{b}$=$\overrightarrow{a}•\overrightarrow{c}$;
(2)对任一向量$\overrightarrow{a}$,有$\overrightarrow{{a}^{2}}$=|$\overrightarrow{a}$|2;
(3)若$\overrightarrow{a}•\overrightarrow{b}$=$\overrightarrow{0}$,则,$\overrightarrow{a}$与$\overrightarrow{b}$中至少有一个为$\overrightarrow{0}$;
(4)|$\overrightarrow{a}•\overrightarrow{b}$|=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|;
(5)$\overrightarrow{a}$与$\overrightarrow{b}$是两个单位向量,则$\overrightarrow{{a}^{2}}$=$\overrightarrow{{b}^{2}}$;
(6)若|$\overrightarrow{a}+\overrightarrow{b}$=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|,则$\overrightarrow{a}$⊥$\overrightarrow{b}$;
(7)($\overrightarrow{a}•\overrightarrow{b}$)$\overrightarrow{c}$=$\overrightarrow{a}$($\overrightarrow{b}•\overrightarrow{c}$)对任意向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$都成立.
分析 根据数量积的计算公式,单位向量的概念,以及向量夹角的概念,相等向量的概念便可判断出每个命题的正误,从而找出正确命题的序号.
解答 解:(1)若$\overrightarrow{a}≠\overrightarrow{0}$,$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{b}>$,$\overrightarrow{a}•\overrightarrow{c}=|\overrightarrow{a}||\overrightarrow{c}|cos<\overrightarrow{a},\overrightarrow{c}>$;
∴$\overrightarrow{a}•\overrightarrow{b}$与$\overrightarrow{a}•\overrightarrow{c}$不一定相等,∴该命题错误;
(2)${\overrightarrow{a}}^{2}=\overrightarrow{a}•\overrightarrow{a}=|\overrightarrow{a}||\overrightarrow{a}|cos0=|\overrightarrow{a}{|}^{2}$,∴该命题正确;
(3)$\overrightarrow{a}•\overrightarrow{b}=0$时,$\overrightarrow{a},\overrightarrow{b}$可都不为0,只要$<\overrightarrow{a},\overrightarrow{b}>=90°$,也能得到$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos90°=0$,∴该命题错误;
(4)$|\overrightarrow{a}•\overrightarrow{b}|=|\overrightarrow{a}||\overrightarrow{b}||cos<\overrightarrow{a},\overrightarrow{b}>|$,而$|cos<\overrightarrow{a},\overrightarrow{b}>|$不一定等于1;
∴$|\overrightarrow{a}•\overrightarrow{b}|=|\overrightarrow{a}||\overrightarrow{b}|$不一定成立,∴该命题错误;
(5)单位向量的长度为1,从而${\overrightarrow{a}}^{2}={\overrightarrow{b}}^{2}=1$,∴该命题正确;
(6)若$|\overrightarrow{a}+\overrightarrow{b}|=|\overrightarrow{a}|+|\overrightarrow{b}|$,则${\overrightarrow{a}}^{2}+2|\overrightarrow{a}||\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{b}>+{\overrightarrow{b}}^{2}$=${\overrightarrow{a}}^{2}+2|\overrightarrow{a}||\overrightarrow{b}|+{\overrightarrow{b}}^{2}$;
∴$2|\overrightarrow{a}||\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{b}>=2|\overrightarrow{a}||\overrightarrow{b}|$;
∴$cos<\overrightarrow{a},\overrightarrow{b}>=1$,或$\overrightarrow{a}=\overrightarrow{0}$,或$\overrightarrow{b}=\overrightarrow{0}$;
即不一定得到$\overrightarrow{a}⊥\overrightarrow{b}$,∴该命题错误;
(7)当$\overrightarrow{c}$,$\overrightarrow{a}$方向不同,且$\overrightarrow{a}•\overrightarrow{b}≠0,\overrightarrow{b}•\overrightarrow{c}≠0$时,显然$(\overrightarrow{a}•\overrightarrow{b})\overrightarrow{c}≠\overrightarrow{a}(\overrightarrow{b}•\overrightarrow{c})$,∴该命题错误;
∴正确命题的序号为:(2)(5).
故答案为:(2)(5).
点评 考查向量数量积的计算公式,向量垂直的概念及垂直的充要条件,以及单位向量的概念,向量数乘的几何意义,相等向量的概念.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案| A. | 2 | B. | 1+$\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | 1 |
| A. | $f(x)=x-\frac{1}{x}$ | B. | f(x)=ex-1 | C. | $f(x)=x+\frac{4}{x}$ | D. | f(x)=tanx |
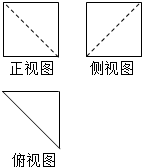 如图是一个多面体的三视图,其中正视图为正方形,俯视图是腰长为2的等腰直角三角形,则该多面体的最大面的面积是4$\sqrt{2}$.
如图是一个多面体的三视图,其中正视图为正方形,俯视图是腰长为2的等腰直角三角形,则该多面体的最大面的面积是4$\sqrt{2}$.