题目内容
若(x+a)6的展开式中x3的系数为160,则
xadx的值为 .
| ∫ | a 1 |
考点:二项式系数的性质,定积分
专题:计算题,二项式定理
分析:在二项式的展开式中令x的幂指数等于3,根据(x+a)6的展开式中x3的系数为160,解得a的值,再利用定积分知识,即可得到结论.
解答:
解:(x+a)6的展开式的通项为Tr+1=
x6-rar,
令6-r=3,则r=3,∴
a3=160,
∴a=2,
∴
xadx=
x2dx=
x3
=
.
故答案为:
.
| C | r 6 |
令6-r=3,则r=3,∴
| C | 3 6 |
∴a=2,
∴
| ∫ | a 1 |
| ∫ | 2 1 |
| 1 |
| 3 |
| | | 2 1 |
| 7 |
| 3 |
故答案为:
| 7 |
| 3 |
点评:本题考查二项展开式的通项公式,求展开式中某项的系数,考查定积分知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在等差数列{an}中,已知a2与a4是方程x2-6x+8=0的两个根,若a4>a2,则a2014=( )
| A、2012 | B、2013 |
| C、2014 | D、2015 |
执行如图所示程序框图,则输出的S的值为( )


| A、21 | B、25 | C、45 | D、93 |
 如图是某个四面体的三视图,若在该四面体的外接球内任取一点,则点落在四面体内的概率为
如图是某个四面体的三视图,若在该四面体的外接球内任取一点,则点落在四面体内的概率为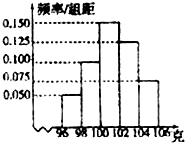 某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分散直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于102克的产品的个数是
某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分散直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于102克的产品的个数是