题目内容
函数f（x）的部分图象如图所示，则f（x）的解析式可以是（ ）分析：由函数图象的对称性可知函数为奇函数，函数过原点，以及利用特殊值的符合是否对应进行判断．
解答：解：由图象可知函数图象关于原点对称，所以函数为奇函数，所以排除D．
当x=
时，f（x）＜0，排除B．
当f（x）=-（x+sinx）时，f'（x）=-1-cosx≤0，
所以此时函数f（x）单调递减，所以排除A．
故选：C．
当x=
| π |
| 2 |
当f（x）=-（x+sinx）时，f'（x）=-1-cosx≤0，
所以此时函数f（x）单调递减，所以排除A．
故选：C．
点评：本题主要考查函数图象的识别和判断，结合函数图象的特点，利用特殊值法是解决函数图象累题目中最常用的方法．复杂的函数图象，还得使用导数进行解决．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
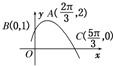已知函数f（x）的部分图象如图所示，则f（x）的解析式可能为（ ）A、f（x）=2cos（
| ||||
B、f（x）=
| ||||
C、f（x）=2sin（
| ||||
D、f（x）=2sin（4x+
|
已知函数f（x）=Asin（ωx+?）（A＞0，ω＞0，0＜?＜π），其导函数f′（x）的部分图象如图所示，则函数f（x）的解析式为
5、已知可导函数f（x）的导函数f′（x）的部分图象如图所示，则函数f（x+1）的部分图象可能是（ ）
函数f（x）的部分图象如图所示，则f（x）的解析式可能是（ ）
（2011•南通模拟）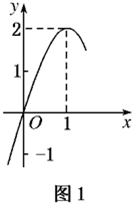
如图所示：图1是定义在R上的二次函数f（x）的部分图象，图2是函数g（x）=loga（x+b）的部分图象．