题目内容
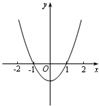5、已知可导函数f（x）的导函数f′（x）的部分图象如图所示，则函数f（x+1）的部分图象可能是（ ）分析：由导函数的图象写出函数f（x）的单调性，由图象的平移变换得到f（x+1）的单调性，选出其图象．
解答：解：由导函数的通图象，
得到f（x）在（-∞，-1）和（1，+∞）上单增；在（-1，1）上单减
∵f（x+1）是由f（x）的图象向左平移1个单位得到
所以f（x+1）在（-∞，-2）和（0，+∞）上单增；在（-2，0）上递减
故选A．
得到f（x）在（-∞，-1）和（1，+∞）上单增；在（-1，1）上单减
∵f（x+1）是由f（x）的图象向左平移1个单位得到
所以f（x+1）在（-∞，-2）和（0，+∞）上单增；在（-2，0）上递减
故选A．
点评：据导函数的符号判断函数的单调区间，当导函数大于0对应函数的得到递增区间，当导函数小于0对应函数的单调递减区间．
练习册系列答案
相关题目
已知可导函数f（x）的导函数为g（x），且满足：①
＞0；②f（2-x）-f（x）=2-2x，记a=f（2）-1，b=f（π）-π+1，c=f（-1）+2，则a，b，c的大小顺序为（ ）
| g(x)-1 |
| x-1 |
| A、a＞b＞c |
| B、a＞c＞b |
| C、b＞c＞a |
| D、b＞a＞c |
已知可导函数f（x）的导函数f'（x）的图象如图所示，给出下列四个结论：