题目内容
矩阵M＝
有特征向量为
，
(1) 求e1和e2对应的特征值；
(2) 对向量α＝
，记作α＝e1＋3e2，利用这一表达式间接计算M4α，M10α.
解：(1) 设向量e1、e2对应的特征值分别为λ1、λ2，则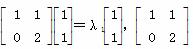
＝
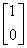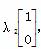
故λ1＝2，λ2＝1，
即向量e1，e2对应的特征值分别是2，1.
(2) 因为α＝e1＋3e2，
所以M4α＝M4(e1＋3e2)＝M4e1＋3M4e2＝λ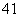
e1＋3λ
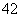e2＝
，
M10α＝M10(e1＋3e2)＝M10e1＋3M10e2＝λ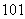
e1＋3λ
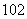e2＝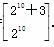
.
练习册系列答案
相关题目
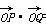＝－2，求实数k的值．
对应的变换作用下得到的点的坐标．
，向量α＝
，β＝
.
β在TM作用下的象；
的特征值及相应的特征向量．
(a>0)对应的变换作用下得到的曲线为x2＋y2＝1.
(t为参数)过的定点．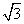
)，求点M的极坐标．
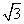，OA＝