题目内容
已知圆C经过点A(-2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)若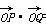 =-2,求实数k的值.
=-2,求实数k的值.
解析: (1)设圆心C(a,a),半径为r.
因为圆C经过点A(-2,0),B(0,2),
所以|AC|=|BC|=r,易得a=0,r=2,
所以圆C的方程是x2+y2=4.
(2)因为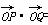 =2×2×cos〈
=2×2×cos〈 〉=-2,且
〉=-2,且 的夹角为∠POQ,
的夹角为∠POQ,
所以cos∠POQ=- ,∠POQ=120°,
,∠POQ=120°,
所以圆心C到直线l:kx-y+1=0的距离d=1,
又d= ,所以k=0.
,所以k=0.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
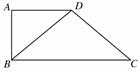
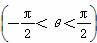 的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P
的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P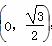 ,则φ的值可以是( )
,则φ的值可以是( )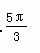 B.
B. 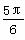
 D.
D. 
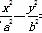 =1和椭圆
=1和椭圆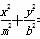 =1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( )
=1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( ) =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4
,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4 .
.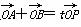 (O为坐标原点),当
(O为坐标原点),当 <
<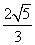 时,求实数t的取值范围.
时,求实数t的取值范围.
 有特征向量为
有特征向量为 ,
, ,记作α=e1+3e2,利用这一表达式间接计算M4α,M10α.
,记作α=e1+3e2,利用这一表达式间接计算M4α,M10α.