题目内容
三棱锥A-BCD的棱长全相等,E是AD中点,则直线CE与直线BD所成角的余弦值为
- A.

- B.

- C.
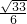
- D.

A
分析:题目要求解的是两条异面直线所成角的余弦值,且给出了棱AD的中点E,可以想到再找AB的中点F,连接两中点EF,得到EF∥BD,则直线CE与直线BD所成角转化为直线CE与直线EF所成角,在三角形CEF中运用余弦定理可求∠CEF的余弦值,则直线CE与直线BD所成角的余弦值可求.
解答: 解:如图,取AB中点F,连接EF,因为E、F分别为AD、AB的中点,则EF为三角形ABD的中位线,所以EF∥BD,
解:如图,取AB中点F,连接EF,因为E、F分别为AD、AB的中点,则EF为三角形ABD的中位线,所以EF∥BD,
所以直线EF与CE所成的角即为直线CE与直线BD所成角,
因为三棱锥A-BCD的棱长全相等,设棱长为2a,则EF=a,
在等边三角形ABC中,因为F为AB的中点,所以CF为边AB上的高,
所以CF= ,
,
则CE=CF= ,
,
在三角形CEF中, =
= .
.
所以,直线CE与直线BD所成角的余弦值为 .
.
故选A.
点评:本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力.在立体几何中找平行线是解决问题的一个重要技巧,这个技巧就是通过三角形的中位线找平行线,如果试题的已知中涉及到多个中点,则找中点是出现平行线的关键技巧,此题是中低档题.
分析:题目要求解的是两条异面直线所成角的余弦值,且给出了棱AD的中点E,可以想到再找AB的中点F,连接两中点EF,得到EF∥BD,则直线CE与直线BD所成角转化为直线CE与直线EF所成角,在三角形CEF中运用余弦定理可求∠CEF的余弦值,则直线CE与直线BD所成角的余弦值可求.
解答:
 解:如图,取AB中点F,连接EF,因为E、F分别为AD、AB的中点,则EF为三角形ABD的中位线,所以EF∥BD,
解:如图,取AB中点F,连接EF,因为E、F分别为AD、AB的中点,则EF为三角形ABD的中位线,所以EF∥BD,所以直线EF与CE所成的角即为直线CE与直线BD所成角,
因为三棱锥A-BCD的棱长全相等,设棱长为2a,则EF=a,
在等边三角形ABC中,因为F为AB的中点,所以CF为边AB上的高,
所以CF=
 ,
,则CE=CF=
 ,
,在三角形CEF中,
 =
= .
.所以,直线CE与直线BD所成角的余弦值为
 .
.故选A.
点评:本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力.在立体几何中找平行线是解决问题的一个重要技巧,这个技巧就是通过三角形的中位线找平行线,如果试题的已知中涉及到多个中点,则找中点是出现平行线的关键技巧,此题是中低档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,各面都是等边三角形的三棱锥A-BCD的棱长为8cm,在棱AB、CD上各有一点E、F,若AE=CF=3cm,则线段EF的长为
如图,各面都是等边三角形的三棱锥A-BCD的棱长为8cm,在棱AB、CD上各有一点E、F,若AE=CF=3cm,则线段EF的长为 已知三棱锥A-BCD的棱长均为a,E为AD的中点,连接CE.
已知三棱锥A-BCD的棱长均为a,E为AD的中点,连接CE. 如图,已知三棱锥A-BCD的棱长都相等,E,F分别是棱AB,CD的中点,则EF与BC所成的角是( )
如图,已知三棱锥A-BCD的棱长都相等,E,F分别是棱AB,CD的中点,则EF与BC所成的角是( )