题目内容
 已知三棱锥A-BCD的棱长均为a,E为AD的中点,连接CE.
已知三棱锥A-BCD的棱长均为a,E为AD的中点,连接CE.(1)请作出AO⊥面BCD于O,则O是△BCD的外心吗?
(2)求二面角A-CD-B的平面角的余弦值.
(3)求CE与底面BCD所成角的正弦值.
分析:(1)要说明O为△BCD为外心,只需说明OB=OC=OD,而AO⊥平面BCD,也就只要这么AB=AC=AD即可,作AO⊥平面BCD,垂足为O,O三角形BCD的中心,连接DO作EO1⊥OD交OD于O1点,连接CO1,即可得到结论;
(2)作AF⊥CD交CD于F,连接OF,根据二面角的平面角的定义可知∠AFO为二面角A-CD-B的平面角,在Rt△AOF中求出此角的余弦值即可;
(3)根据线面垂直的判定定理可知EO1⊥平面BCD,从而∠ECO1是CE与平面BCD所成的角,在Rt△EO1C中,求出此角的正弦值即可.
(2)作AF⊥CD交CD于F,连接OF,根据二面角的平面角的定义可知∠AFO为二面角A-CD-B的平面角,在Rt△AOF中求出此角的余弦值即可;
(3)根据线面垂直的判定定理可知EO1⊥平面BCD,从而∠ECO1是CE与平面BCD所成的角,在Rt△EO1C中,求出此角的正弦值即可.
解答:解:(1)作AO⊥平面BCD,垂足为O,O三角形BCD的中心.
连接DO作EO1⊥OD交OD于O1点,连接CO1
∵AB=AC=AD=a,AO⊥平面BCD∴O为△BCD为外心
(2)作AF⊥CD交CD于F,连接OF.
∵AO⊥平面BCD∴AO⊥CD
又∵AF⊥CD∴CD⊥平面AFO
∴CD⊥OF∴∠AFO为二面角A-CD-B的平面角.
在Rt△AOF中AF=
a,AO=
a
∴cos∠AFO=
.
(3)∴OD=
×
a=
a∴在Rt△AOD中,AO=
=
a
∵AE=DE,EO1∥AO∴EO1=
AO=
a
∵AO⊥平面BCD,EO1∥AO∴EO1⊥平面BCD
∴∠ECO1是CE与平面BCD所成的角
在Rt△EO1C中,sin∠ECO1=
=
=
连接DO作EO1⊥OD交OD于O1点,连接CO1
∵AB=AC=AD=a,AO⊥平面BCD∴O为△BCD为外心
(2)作AF⊥CD交CD于F,连接OF.
∵AO⊥平面BCD∴AO⊥CD
又∵AF⊥CD∴CD⊥平面AFO
∴CD⊥OF∴∠AFO为二面角A-CD-B的平面角.
在Rt△AOF中AF=
| ||
| 2 |
| ||
| 3 |
∴cos∠AFO=
| 1 |
| 3 |
(3)∴OD=
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
a2-(
|
| ||
| 3 |
∵AE=DE,EO1∥AO∴EO1=
| 1 |
| 2 |
| ||
| 6 |
∵AO⊥平面BCD,EO1∥AO∴EO1⊥平面BCD
∴∠ECO1是CE与平面BCD所成的角
在Rt△EO1C中,sin∠ECO1=
| EO1 |
| CE |
| ||||
|
| ||
| 3 |
点评:本题主要考查了二面角的度量,以及线面所成角,同时考查了空间想象能力,推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
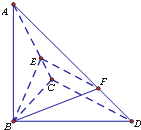 已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是直线AC,AD上的点,且
已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是直线AC,AD上的点,且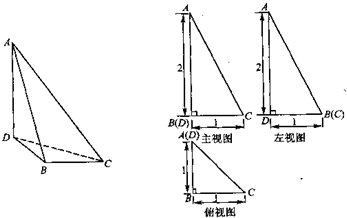 (2009•大连一模)已知三棱锥A-BCD及其三视图如图所示.
(2009•大连一模)已知三棱锥A-BCD及其三视图如图所示.