题目内容
若40个数据的平方和是30,平均数是
,则这组数据的标准差为( )
| ||
| 2 |
A、
| ||
| B、1 | ||
| C、2 | ||
D、
|
考点:极差、方差与标准差
专题:计算题,概率与统计
分析:根据方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2]进行计算即可.
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
解答:
解:∵方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2]
=
[x12+x22+…+xn2+n
2-2
(x1+x2+…+xn)]
=
[x12+x22+…+xn2+n
2-2n
2]
=
[x12+x22+…+xn2]-
2
=
×30-(
)2=
,
∴这组数据的标准差是
.
故选:A.
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
=
| 1 |
| n |
. |
| x |
. |
| x |
=
| 1 |
| n |
. |
| x |
. |
| x |
=
| 1 |
| n |
. |
| x |
=
| 1 |
| 40 |
| ||
| 2 |
| 1 |
| 4 |
∴这组数据的标准差是
| 1 |
| 2 |
故选:A.
点评:本题考查了方差的计算问题,解题时根据平均数与方差的计算公式进行计算即可,是基础题.

练习册系列答案
相关题目
不等式|2x-1|>3的解集是( )
| A、{x|-1<x<2} |
| B、{x|-2<x<1} |
| C、{x|x>2或x<-1} |
| D、{x|x>-1或x<2} |
i是虚数单位,若复数Z=i(1+3i),则复数Z的虚部是( )
| A、-3 | B、3i | C、1 | D、i |
下列各式中,最小值是2的是( )
A、x+
| ||||
B、
| ||||
C、
| ||||
D、2-3x-
|
已知两条直线l1:ax+3y-3=0,l2:4x+6y-1=0.若l1∥l2,则a=( )
| A、5 | B、4 | C、3 | D、2 |
从1,2,3,4,5这五个数中,每次取出两个不同的数记为a,b,则共可得到ln
的不同值的个数为( )
| b |
| a |
| A、20 | B、19 | C、18 | D、17 |
 在三棱锥A-BCD中,AC⊥底面BCD,BD⊥DC,BD=DC,AC=1,∠ABC=30°,则C到平面ABD的距离是( )
在三棱锥A-BCD中,AC⊥底面BCD,BD⊥DC,BD=DC,AC=1,∠ABC=30°,则C到平面ABD的距离是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
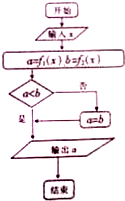 已知函数f1(x)=x,f2(x)=
已知函数f1(x)=x,f2(x)=