题目内容
双曲线C:x2 – y2 = a2的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于A、B两点,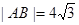 ,则双曲线C的方程为__________.
,则双曲线C的方程为__________.
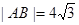 ,则双曲线C的方程为__________.
,则双曲线C的方程为__________.
试题分析:易知抛物线y2=16x的准线方程为x="-4,"
 ,因为
,因为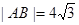 ,所以
,所以 ,解得
,解得 ,所以双曲线C的方程为
,所以双曲线C的方程为 。
。点评:熟记双曲线与抛物线的简单性质是做此题的前提条件。属于基础题型。

练习册系列答案
相关题目
题目内容
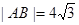 ,则双曲线C的方程为__________.
,则双曲线C的方程为__________.
 ,因为
,因为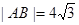 ,所以
,所以 ,解得
,解得 ,所以双曲线C的方程为
,所以双曲线C的方程为 。
。