题目内容
(本小题满分14分)
已知椭圆的中心是坐标原点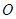 ,焦点在x轴上,离心率为
,焦点在x轴上,离心率为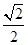 ,又椭圆上任一点到两焦点的距离和为
,又椭圆上任一点到两焦点的距离和为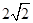 ,过点M(0,
,过点M(0,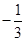 )与x轴不垂直的直线
)与x轴不垂直的直线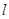 交椭圆于P、Q两点.
交椭圆于P、Q两点.
(1)求椭圆的方程;
(2)在y轴上是否存在定点N,使以PQ为直径的圆恒过这个点?若存在,求出N的坐标,若不存在,说明理由.
已知椭圆的中心是坐标原点
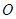 ,焦点在x轴上,离心率为
,焦点在x轴上,离心率为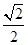 ,又椭圆上任一点到两焦点的距离和为
,又椭圆上任一点到两焦点的距离和为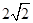 ,过点M(0,
,过点M(0,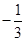 )与x轴不垂直的直线
)与x轴不垂直的直线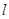 交椭圆于P、Q两点.
交椭圆于P、Q两点.(1)求椭圆的方程;
(2)在y轴上是否存在定点N,使以PQ为直径的圆恒过这个点?若存在,求出N的坐标,若不存在,说明理由.
(1) 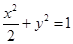 (2)先假设存在,联立方程组,利用
(2)先假设存在,联立方程组,利用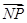 ·
·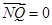 可以求出存在
可以求出存在
N(0,1)满足要求
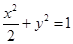 (2)先假设存在,联立方程组,利用
(2)先假设存在,联立方程组,利用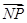 ·
·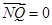 可以求出存在
可以求出存在N(0,1)满足要求
试题分析:(1)因为离心率为
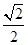 ,又
,又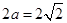 ,∴a=
,∴a=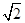 ,c=1,
,c=1,故b=1,故椭圆的方程为
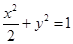 . ……4分
. ……4分(2)由题意设直线
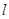 的方程为y=kx-
的方程为y=kx-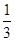 ,
,联立方程
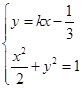 得(2k2+1)x2-
得(2k2+1)x2-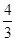 kx-
kx-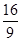 =0,
=0,设P(x1, y1),Q(x2, y2),
则x1+x2=
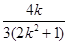 ,x1·x2=
,x1·x2=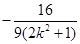 , ……8分
, ……8分假设在y轴上存在定点N(0,m)满足题设,则
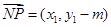 ,
,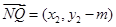 ,
,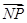 ·
·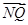 = x1x2+(y1-m)(y2-m)= x1x2+ y1y2-m(y1+y2) +m2
= x1x2+(y1-m)(y2-m)= x1x2+ y1y2-m(y1+y2) +m2= x1x2+(kx1-
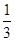 )( kx2-
)( kx2-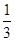 )-m(kx1-
)-m(kx1-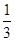 + kx2-
+ kx2-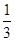 ) +m2
) +m2=(k2+1) x1x2-k(
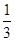 +m)(x1+x2)+m2+
+m)(x1+x2)+m2+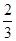 m+
m+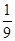
=
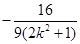 -k(
-k(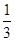 +m)
+m)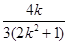 +m2+
+m2+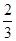 m+
m+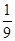
=
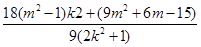 , ……12分
, ……12分由假设得对于任意的k∈R,
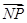 ·
·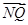 =0恒成立,
=0恒成立,即
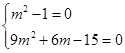 解得m=1,
解得m=1,因此,在y轴上存在定点N,
使得以PQ为直径的圆恒过这个点,点N的坐标为(0,1). ……14分
点评:对于探究性问题,一般是先假设存在,然后计算,如果能求出,则说明存在,如果求不出或得出矛盾,则说明不存在.

练习册系列答案
相关题目
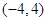 的抛物线的标准方程是
的抛物线的标准方程是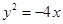
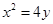
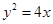 或
或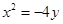
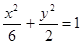 的右焦点重合,则此抛物线的方程是( )
的右焦点重合,则此抛物线的方程是( )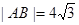 ,则双曲线C的方程为__________.
,则双曲线C的方程为__________.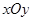 内的点
内的点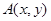 (不是原点),
(不是原点),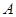 的“对偶点”
的“对偶点”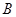 是指:满足
是指:满足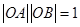 且在射线
且在射线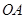 上的那个点. 则圆心在原点的圆的对偶图形( )
上的那个点. 则圆心在原点的圆的对偶图形( )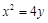 的焦点
的焦点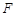 和点
和点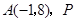 为抛物线上一点,则
为抛物线上一点,则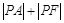 的最小值是( )
的最小值是( ) ,
, ,△
,△ 的周长是
的周长是 ,则
,则 的顶点
的顶点 的轨迹方程为___ ________
的轨迹方程为___ ________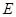 的焦点在
的焦点在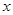 轴上,离心率为
轴上,离心率为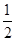 ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点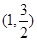 .
.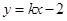 与椭圆
与椭圆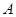 、
、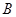 两点,
两点, 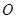 为原点,在
为原点,在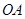 、
、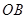 上分别存在异于
上分别存在异于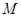 、
、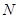 ,使得
,使得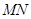 为直径的圆外,求直线斜率
为直径的圆外,求直线斜率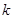 的取值范围.
的取值范围.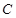 中心在原点,一个焦点为
中心在原点,一个焦点为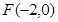 ,且长轴长与短轴长的比是
,且长轴长与短轴长的比是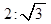 。
。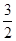 的直线
的直线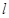 ,使直线
,使直线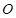 与直线
与直线