题目内容
过椭圆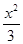 +y2=1的一个焦点
+y2=1的一个焦点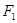 的直线与椭圆交于
的直线与椭圆交于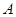 、
、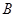 两点,则
两点,则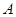 、
、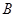 与椭圆的另一焦点
与椭圆的另一焦点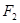 构成的△
构成的△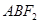 的周长为 .
的周长为 .
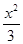 +y2=1的一个焦点
+y2=1的一个焦点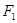 的直线与椭圆交于
的直线与椭圆交于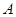 、
、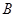 两点,则
两点,则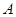 、
、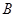 与椭圆的另一焦点
与椭圆的另一焦点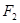 构成的△
构成的△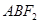 的周长为 .
的周长为 .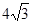
试题分析:由椭圆的定义知:△
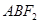 的周长为为4a,即
的周长为为4a,即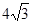 。
。点评:直接考查椭圆的定义:椭圆上任何一点到两焦点的距离和为2a。属于基础题型。

练习册系列答案
相关题目
题目内容
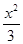 +y2=1的一个焦点
+y2=1的一个焦点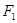 的直线与椭圆交于
的直线与椭圆交于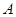 、
、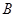 两点,则
两点,则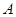 、
、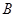 与椭圆的另一焦点
与椭圆的另一焦点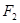 构成的△
构成的△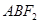 的周长为 .
的周长为 .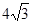
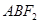 的周长为为4a,即
的周长为为4a,即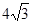 。
。